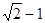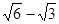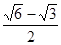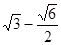题目内容
(本题满分14分
已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆
于另一点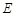 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
已知椭圆
 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心,椭圆的短半轴长为半径的圆与直线
 相切.
相切.⑴求椭圆C的方程;
⑵设
 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆
于另一点
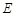 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;⑶在⑵的条件下,证明直线
 与
与 轴相交于定点.
轴相交于定点.⑴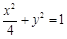 ;
;
⑵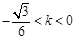 或
或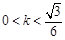 ;
;
⑶见解析
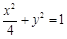 ;
;⑵
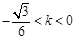 或
或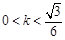 ;
;⑶见解析
本题考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是确定几何量之间的关系,利用直线与椭圆联立,结合韦达定理求解
(1)根据椭圆的性质,离心率得到参数a,c的关系,然后利用线与圆相切得到参数b的值,进而得到椭圆的方程。
(2)设出直线与椭圆的方程联立方程组,结合韦达定理,和判别式大于零得到直线的斜率的范围。
(3)表示直线ME的方程,以及结合点的坐标的对称关系,得到k的关系式,进而得到直线 与
与 轴相交于定点
轴相交于定点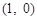
解:⑴由题意知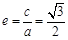 ,
,
所以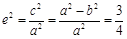 ,即
,即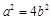 ,
,
又因为 ,所以
,所以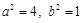 ,
,
故椭圆 的方程为
的方程为 :
: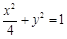 .-----------4分
.-----------4分
⑵由题意知直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为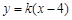 ①
①
联立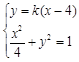 消去
消去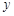 得:
得: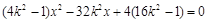 ,
,
由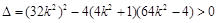 得
得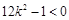 ,
,
又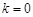 不合题意,
不合题意,
所以直线 的斜率的取值范围是
的斜率的取值范围是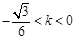 或
或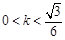 .---8分
.---8分
⑶设点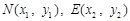 ,则
,则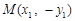 ,
,
直线 的方程为
的方程为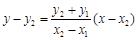 ,
,
令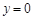 ,得
,得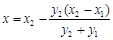 ,
,
将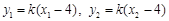 代入整理,得
代入整理,得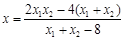 . ②
. ②
由得①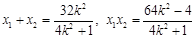 代入②整理,得
代入②整理,得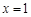 ,
,
所以直线 与
与 轴相交于定点
轴相交于定点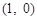 . ----------------14分
. ----------------14分
(1)根据椭圆的性质,离心率得到参数a,c的关系,然后利用线与圆相切得到参数b的值,进而得到椭圆的方程。
(2)设出直线与椭圆的方程联立方程组,结合韦达定理,和判别式大于零得到直线的斜率的范围。
(3)表示直线ME的方程,以及结合点的坐标的对称关系,得到k的关系式,进而得到直线
 与
与 轴相交于定点
轴相交于定点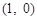
解:⑴由题意知
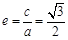 ,
,所以
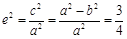 ,即
,即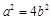 ,
,又因为
 ,所以
,所以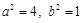 ,
,故椭圆
 的方程为
的方程为 :
: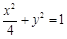 .-----------4分
.-----------4分⑵由题意知直线
 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为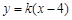 ①
①联立
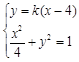 消去
消去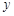 得:
得: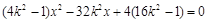 ,
,由
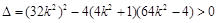 得
得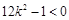 ,
,又
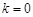 不合题意,
不合题意,所以直线
 的斜率的取值范围是
的斜率的取值范围是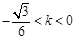 或
或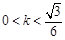 .---8分
.---8分⑶设点
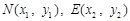 ,则
,则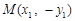 ,
,直线
 的方程为
的方程为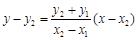 ,
,令
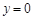 ,得
,得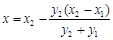 ,
,将
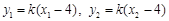 代入整理,得
代入整理,得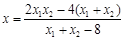 . ②
. ②由得①
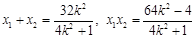 代入②整理,得
代入②整理,得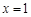 ,
,所以直线
 与
与 轴相交于定点
轴相交于定点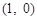 . ----------------14分
. ----------------14分
练习册系列答案
相关题目
 ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围; 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
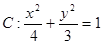 的右顶点是
的右顶点是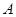 ,上下两个顶点分别为
,上下两个顶点分别为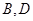 ,四边形
,四边形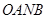 是矩形(
是矩形(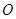 为原点),点
为原点),点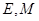 分别为线段
分别为线段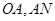 的中点.
的中点.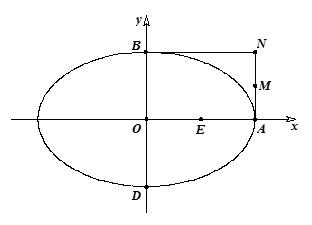
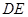 与直线
与直线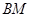 的交点在椭圆
的交点在椭圆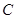 上;
上;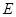 的直线交椭圆于
的直线交椭圆于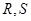 两点,
两点,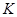 为
为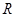 关于
关于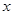 轴的对称点(
轴的对称点(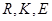 不共线),
不共线),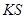 是否经过
是否经过 :
: 的离心率是
的离心率是 ,其左、右顶点分别为
,其左、右顶点分别为 ,
, ,
, 为短轴的端点,△
为短轴的端点,△ 的面积为
的面积为 .
. 为椭圆
为椭圆 是椭圆
是椭圆 ,
, 与直线
与直线 分别交于
分别交于 ,
, 两点,证明:以
两点,证明:以 为直径的圆与直线
为直径的圆与直线 相切于点
相切于点 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点. 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;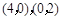 ,椭圆的方程是
,椭圆的方程是 或
或



 是椭圆的一部分,灯丝位于椭圆的一个焦点
是椭圆的一部分,灯丝位于椭圆的一个焦点 上,片门位于另一个焦点
上,片门位于另一个焦点 上,由椭圆一个焦点
上,由椭圆一个焦点 ,
, ,
, 试建立适当的坐标系,求截口
试建立适当的坐标系,求截口 为椭圆
为椭圆 的左、右焦点,若
的左、右焦点,若 为椭圆上一点,且△
为椭圆上一点,且△ 的内切圆的周长等于
的内切圆的周长等于 ,则满足条件的点
,则满足条件的点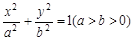 的焦点为
的焦点为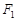 和
和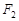 ,过点
,过点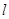 交椭圆于
交椭圆于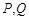 两点,
两点,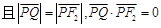 ,则椭圆的离心率为( )
,则椭圆的离心率为( )