题目内容
(本小题12分)
已知椭圆 ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 的上方,
的上方,
(1)求直线 与
与 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围;
(2)证明: 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
已知椭圆
 ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 的上方,
的上方,(1)求直线
 与
与 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围;(2)证明:
 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
(1)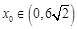
(2)见解析
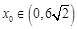
(2)见解析
(1)设直线l的方程为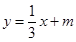 ,然后求出它与x轴交点横坐标
,然后求出它与x轴交点横坐标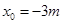 ,再让直线l的方程与椭圆方程联立,
,再让直线l的方程与椭圆方程联立,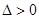 和点P在l的上方两个条件确定m的取值范围,然后转化为函数值域问题来解决。
和点P在l的上方两个条件确定m的取值范围,然后转化为函数值域问题来解决。
(2) 先由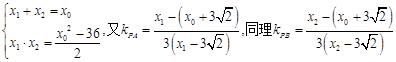 ,得到
,得到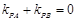 ,这说明了
,这说明了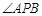 的角平分线与x轴垂直,问题到此基本得以解决。
的角平分线与x轴垂直,问题到此基本得以解决。
解:(1)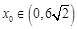
(2)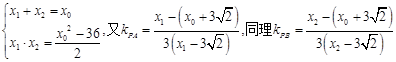
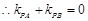 ,又
,又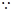 点
点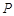 在直线
在直线 的上方,故
的上方,故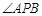 的角平分线是平行于
的角平分线是平行于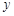 轴的直线,
轴的直线,
故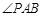 的内切圆圆心在直线
的内切圆圆心在直线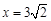 上.
上.
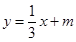 ,然后求出它与x轴交点横坐标
,然后求出它与x轴交点横坐标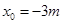 ,再让直线l的方程与椭圆方程联立,
,再让直线l的方程与椭圆方程联立,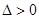 和点P在l的上方两个条件确定m的取值范围,然后转化为函数值域问题来解决。
和点P在l的上方两个条件确定m的取值范围,然后转化为函数值域问题来解决。(2) 先由
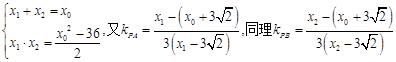 ,得到
,得到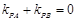 ,这说明了
,这说明了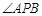 的角平分线与x轴垂直,问题到此基本得以解决。
的角平分线与x轴垂直,问题到此基本得以解决。解:(1)
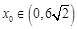
(2)
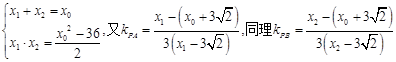
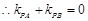 ,又
,又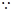 点
点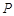 在直线
在直线 的上方,故
的上方,故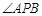 的角平分线是平行于
的角平分线是平行于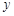 轴的直线,
轴的直线,故
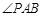 的内切圆圆心在直线
的内切圆圆心在直线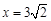 上.
上.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 :
: 的离心率为
的离心率为 ,以原点为圆心,
,以原点为圆心, 相切.
相切. ,
, 、
、 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆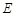 ,求直线
,求直线 与
与 的一个焦点是
的一个焦点是 ,且截直线
,且截直线 所得弦长为
所得弦长为 ,求该椭圆的方程.
,求该椭圆的方程. 中,椭圆
中,椭圆 为
为
 ,且线段
,且线段 恰以点
恰以点 为中点,求直线
为中点,求直线 的直线
的直线 (非
(非 轴)与椭圆
轴)与椭圆 试问在
试问在 ,使
,使 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点 的坐标及实数
的坐标及实数 与双曲线
与双曲线 的左右两支分别交于
的左右两支分别交于 、
、 两点,与双曲线
两点,与双曲线 的右准线相交于
的右准线相交于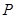 点,
点, 为右焦点,若
为右焦点,若 ,又
,又 ,则实数
,则实数 的值为
的值为
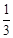

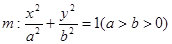 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为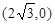 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且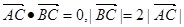
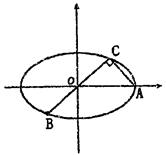
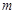 的方程;
的方程;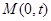 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,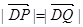 ,求实数t的取值范围.
,求实数t的取值范围. 的左、右顶点分别A、B,椭圆过点(0,1)且离心率
的左、右顶点分别A、B,椭圆过点(0,1)且离心率 .
. 轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线
轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线 轴,连结AQ并延长交直线
轴,连结AQ并延长交直线 于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
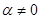 的直线
的直线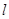 过椭圆
过椭圆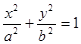
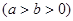 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则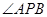 为 ( )
为 ( )