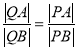题目内容
【题目】把一个均匀的正方体骰子抛掷两次,观察出现的点数,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() ,设直线
,设直线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求直线![]() 和直线
和直线![]() 没有交点的概率;
没有交点的概率;
(2)求直线![]() 和直线
和直线![]() 的交点在第一象限的概率.
的交点在第一象限的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)把一颗骰子投掷两次,第一次出现的点数记为![]() ,第二次出现的点数记为
,第二次出现的点数记为![]() ,则不同的结果数是36种,然后求出两直线
,则不同的结果数是36种,然后求出两直线![]() 、
、![]() 平行的情况为
平行的情况为![]() ,找出符合条件的所有基本事件数,由公式计算出概率.
,找出符合条件的所有基本事件数,由公式计算出概率.
(2)联立直线方程得到交点坐标,根据交点在第一象限,得到不等式组,列出满足条件的数对,再用古典概型的概率计算公式计算可得.
解:骰子抛掷两次的结果记为![]() ,则所有可能的情况共有
,则所有可能的情况共有![]() 种情况(如图)
种情况(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)直线![]() 和直线
和直线![]() 没有交点即
没有交点即![]() ,所以
,所以![]() ,
,
共有![]() ,
,![]() ,
,![]() 共
共![]() 种不同结果.
种不同结果.
因此所求概率![]() .
.
(2)![]() 得
得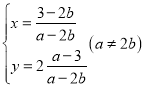 ,
,
由![]() 得
得 或者
或者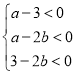 ,
,
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共
共![]() 种不同结果.
种不同结果.
因此所求概率![]() .
.

练习册系列答案
相关题目
【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片.把每列标号最小的卡片选出,将这些卡片中标号最大的数设为a;把每行标号最大的卡片选出,将这些卡片中标号最小的数设为b.
甲同学认为a有可能比b大,乙同学认为a和b有可能相等.那么甲乙两位同学中说法正确的同学是_______.