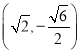题目内容
【题目】定义域为R的偶函数f(x)满足对x∈R，有f(x+2)＝f(x)﹣f(1)，且当x∈[2，3]时，f(x)＝﹣2x2+12x﹣18，若函数y＝f(x)﹣loga(|x|+1)至少有6个零点，则a的取值范围是( )
A.(0，
)B.(0，
)C.(0，
)D.(0，
)
【答案】B
【解析】
令x＝﹣1，求出f(1)＝0，得出函数f(x)的周期为2，画出f(x)和y＝loga(|x|+1)的图象，利用数形结合的方法进行求解；
解：∵f(x+2)＝f(x)﹣f(1)，∴f(﹣1+2)＝f(﹣1)﹣f(1)，即f(1)＝f(﹣1)﹣f(1)，∴2f(1)＝f(﹣1)．
∵f(x)是定义域为R的偶函数，∴f(﹣1)＝f(1)，∴2f(1)＝f(1)，f(1)＝0．∴f(x+2)＝f(x)，∴f(x)是周期为2的偶函数．
作出f(x)和y＝loga(|x|+1)的图象如图所示：
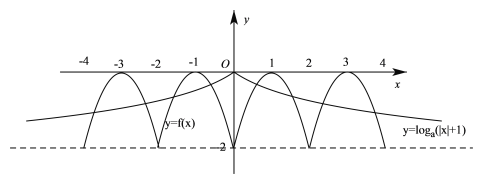
∵函数y＝f(x)﹣loga(|x|+1)至少有6个零点，∴0＜a＜1．
∴loga(2+1)＞﹣2，解得0＜a
．
故选：B．
练习册系列答案
相关题目
