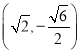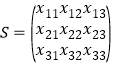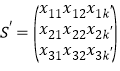题目内容
【题目】《九章算术》是我国古代数学文化的优秀遗产，数学家刘徽在注解《九章算术》时，发现当圆内接正多边行的边数无限增加时，多边形的面积可无限逼近圆的面积，为此他创立了割圆术，利用割圆术，刘徽得到了圆周率精确到小数点后四位3.1416，后人称3.14为徽率，如图是利用刘徽的割圆术设计的程序框图，若结束程序时，则输出的
为（ ）（
，
，
）
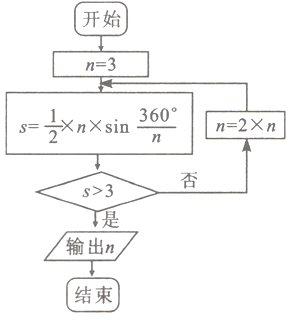
A. 6 B. 12 C. 24 D. 48
【答案】C
【解析】
列出循环过程中s与n的数值，满足判断框的条件即可结束循环．
模拟执行程序，可得：
n＝3，S
3×sin120°
，
不满足条件S＞3，执行循环体，n＝6，S6×sin60°
，
不满足条件S＞3，执行循环体，n＝12，S12×sin30°＝3，
不满足条件S＞3，执行循环体，n＝24，S24×sin15°≈12×0.2588＝3.1056，
满足条件S＞3，退出循环，输出n的值为24．
故选：C．
练习册系列答案
相关题目
