题目内容
已知数列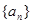 ,
,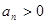 ,
,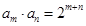 ,
,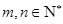 .
.
(1)求证: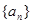 为等比数列,并求出通项公式
为等比数列,并求出通项公式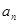 ;
;
(2)记数列 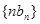 的前
的前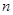 项和为
项和为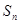 且
且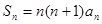 ,求
,求
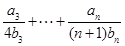 .
.
(1)见解析;(2)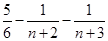 .
.
解析试题分析:(1)由题意关系式先求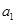 ,再求
,再求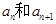 的表达式,从而可得
的表达式,从而可得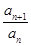 的比值,即为公比,可得数列
的比值,即为公比,可得数列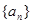 的通项公式;(2)先由数列
的通项公式;(2)先由数列 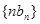 的前
的前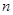 项和为
项和为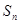 的表达式计算
的表达式计算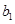 的值,再有
的值,再有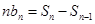 关系式计算
关系式计算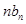 ,即可得
,即可得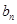 ,然后再得所求和的通项,即可求和.
,然后再得所求和的通项,即可求和.
试题解析:(Ⅰ)由题意得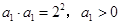 ,得
,得 . 1分
. 1分
且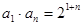 ,
, 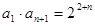 ,
,
所以 ,且
,且 ,所以
,所以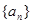 为等比数列. 3分
为等比数列. 3分
所以通项公式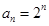 . 5分
. 5分
(Ⅱ)由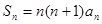 ,当
,当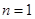 时,得
时,得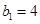 ; 6分
; 6分
当 时,
时,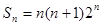 , ①
, ① , ②
, ②
①-②得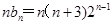 ,即
,即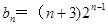 . 9分
. 9分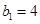 满足上式,所以
满足上式,所以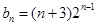 . 10分
. 10分
所以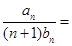
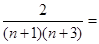
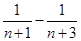 . 12分
. 12分
所以
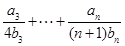


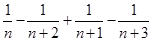
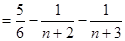 . 14分
. 14分
考点:1、数列的递推公式;2、等比数列的通项公式;3、由前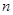 项和求通项法;4、拆项求和法.
项和求通项法;4、拆项求和法.

练习册系列答案
相关题目
 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: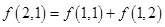 ;
;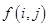 为数表中第
为数表中第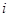 行的第
行的第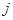 个数.
个数.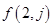 和
和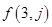 ;
;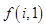 关于
关于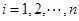 )的表达式.
)的表达式.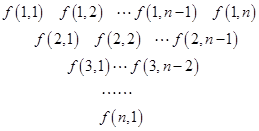
 ,
,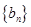 满足
满足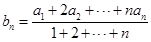
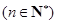 .
.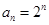 ,求数列
,求数列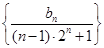 的前
的前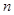 项和
项和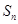 .
. }满足
}满足 -
-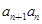 -2
-2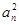 =0,n∈N﹡,且
=0,n∈N﹡,且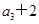 是a2,a4的等差中项.
是a2,a4的等差中项.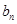 =
=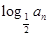 ,
,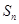 =b1+b2+…+
=b1+b2+…+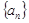 满足
满足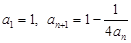 ,其中
,其中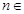 N*.
N*.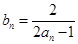 ,求证:数列
,求证:数列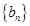 是等差数列,并求出
是等差数列,并求出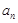 ;
;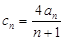 ,数列
,数列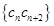 的前
的前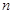 项和为
项和为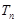 ,是否存在正整数
,是否存在正整数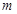 ,使得
,使得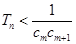 对于
对于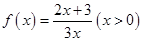 ,数列
,数列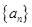 满足
满足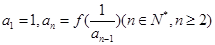 .
.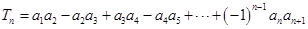 ,若
,若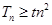 对
对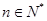 恒成立,求实数
恒成立,求实数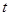 的取值范围;
的取值范围;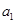 为首项,公比为
为首项,公比为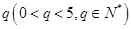 的数列
的数列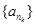 ,
,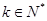 ,使得数列
,使得数列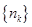 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.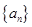 满足递推式:
满足递推式: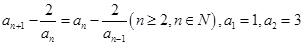 .
.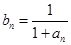 ,求
,求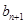 与
与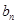 的递推关系(用
的递推关系(用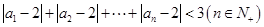 .
. 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在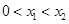 ,使得不等式
,使得不等式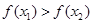 成立 设数列
成立 设数列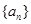 的前
的前 项和为
项和为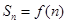
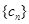 中,所有满足
中,所有满足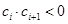 的正整数
的正整数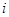 的个数称为这个数列
的个数称为这个数列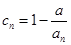 (
(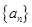 满足
满足 ,且
,且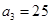 .
. 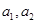
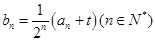 ,且{
,且{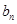 }为等差数列?若存在,求出t的值;若不存在,说明理由.
}为等差数列?若存在,求出t的值;若不存在,说明理由.