题目内容
已知函数 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在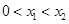 ,使得不等式
,使得不等式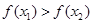 成立 设数列
成立 设数列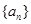 的前
的前 项和为
项和为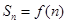
(1)求数列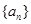 的通项公式;
的通项公式;
(2)设各项均不为零的数列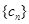 中,所有满足
中,所有满足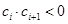 的正整数
的正整数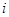 的个数称为这个数列
的个数称为这个数列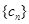 的变号数,令
的变号数,令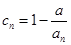 (
( 为正整数),求数列
为正整数),求数列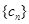 的变号数
的变号数
(1)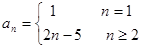 ;(2)3
;(2)3
解析试题分析:(1)由一元二次不等式的解集有且只有一个元素可判断对应方程的判别式等于零,再根据单调性确定参数 的值,然后求数列
的值,然后求数列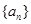 的通项公式;(2)根据新定义,代入解不等式即可,需要注意
的通项公式;(2)根据新定义,代入解不等式即可,需要注意 的特殊性
的特殊性
试题解析:(1)由① 的解集有且只有一个元素知
的解集有且只有一个元素知 或
或 4分
4分
当 时,函数
时,函数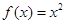 在
在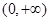 上递增,此时不满足条件② 6分
上递增,此时不满足条件② 6分
综上可知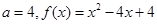
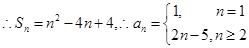 8分
8分
(2)由条件可知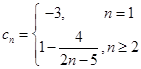
当 时,令
时,令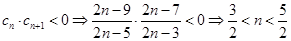 或
或
所以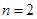 或
或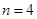 13分
13分
又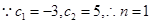 时,也有
时,也有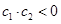 15分
15分
综上可得数列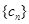 的变号数为3 16分
的变号数为3 16分
考点:二次函数,数列

练习册系列答案
相关题目
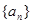 ,
,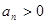 ,
,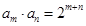 ,
,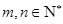 .
.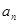 ;
;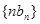 的前
的前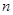 项和为
项和为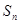 且
且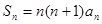 ,求
,求
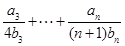 .
. 是等差数列,且
是等差数列,且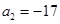 ,
,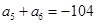 ;又若
;又若 是各项为正数的等比数列,且满足
是各项为正数的等比数列,且满足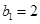 ,其前
,其前 项和为
项和为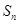 ,
,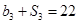 .
.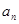 ,
,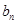 ;
;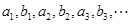 的前
的前 ,求
,求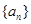 的前
的前 项和为
项和为 ,
,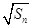 是
是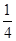 与
与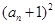 的等比中项.
的等比中项.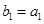 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前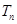 .
.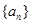 的各项均为正数,
的各项均为正数,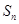 为其前
为其前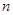 项和,对于任意的
项和,对于任意的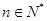 ,满足关系式
,满足关系式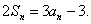
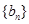 的通项公式是
的通项公式是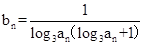 ,前
,前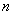 项和为
项和为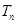 ,求证:对于任意的正整数
,求证:对于任意的正整数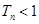 .
.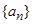 中,
中,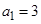 ,前
,前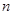 和
和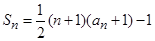
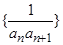 的前
的前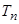 ,是否存在实数
,是否存在实数 ,使得
,使得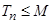 对一切正整数
对一切正整数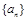 和公比为
和公比为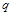
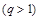 的等比数列
的等比数列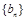 满足:
满足: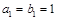 ,
,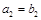 ,
, .
.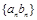 的前
的前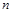 项和为
项和为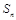 ,且对任意
,且对任意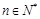 均有
均有 成立,试求实数
成立,试求实数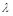 的取值范围.
的取值范围.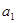 =2,点(
=2,点(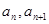 )在函数
)在函数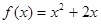 的图像上,其中
的图像上,其中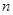 =
=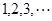 .
.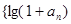 }是等比数列;
}是等比数列;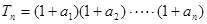 ,求
,求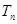 及数列{
及数列{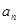 }的通项公式;
}的通项公式;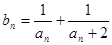 ,求数列{
,求数列{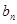 }的前n项和
}的前n项和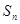 ,并证明
,并证明 .
.