题目内容
已知数列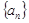 满足
满足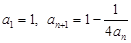 ,其中
,其中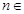 N*.
N*.
(Ⅰ)设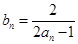 ,求证:数列
,求证:数列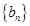 是等差数列,并求出
是等差数列,并求出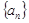 的通项公式
的通项公式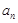 ;
;
(Ⅱ)设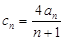 ,数列
,数列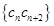 的前
的前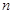 项和为
项和为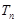 ,是否存在正整数
,是否存在正整数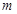 ,使得
,使得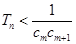 对于
对于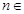 N*恒成立,若存在,求出
N*恒成立,若存在,求出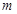 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
(Ⅰ)详见解析;(Ⅱ)3
解析试题分析:(Ⅰ)利用等差数列的定义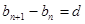 即可证明该数列导数是等差数列,然后求首项、公差即可得出的通项公式;(Ⅱ)首先求得
即可证明该数列导数是等差数列,然后求首项、公差即可得出的通项公式;(Ⅱ)首先求得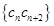 的通项公式,然后根据裂项求和得
的通项公式,然后根据裂项求和得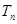 ,根据题意得出关于
,根据题意得出关于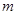 不等式解之即可.
不等式解之即可.
试题解析:(I)证明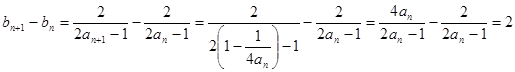 ,
,
所以数列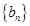 是等差数列,
是等差数列,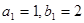 ,因此
,因此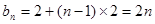 ,
,
由 得
得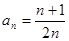 . 8分
. 8分
(II)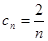 ,
, ,
,
所以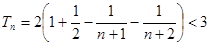 ,
,
依题意要使 对于
对于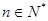 恒成立,只需
恒成立,只需
解得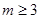 或
或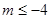 ,所以
,所以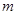 的最小值为
的最小值为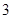 15分
15分
考点:1.等差数列;2.裂项求和.

练习册系列答案
相关题目
 )项,且
)项,且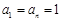 ,对每个i (1≤i≤
,对每个i (1≤i≤ ,i
,i N),均有
N),均有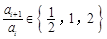 .
.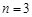 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);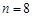 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数.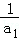 +
+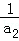 +…+
+…+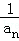 <
<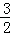 .
.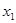 (
( 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为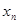 ,该年的增长量
,该年的增长量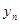 和
和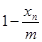 的乘积成正比,比例系数为
的乘积成正比,比例系数为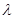
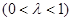 其中
其中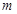 =200万.
=200万.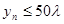 ;
;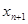 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.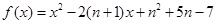 .
.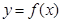 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列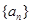 ,求证:
,求证: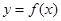 的图像的顶点到
的图像的顶点到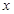 轴的距离构成数列
轴的距离构成数列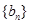 ,求
,求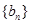 的前
的前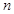 项和
项和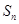 .
.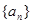 ,
,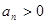 ,
,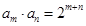 ,
,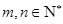 .
.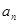 ;
;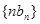 的前
的前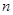 项和为
项和为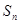 且
且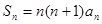 ,求
,求
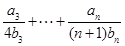 .
. 的首项
的首项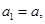 其中
其中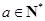 ,
,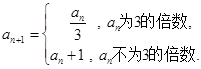 令集合
令集合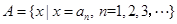 .
.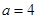 ,写出集合
,写出集合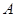 中的所有的元素;
中的所有的元素;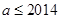 ,且数列
,且数列 的所有可能取值构成的集合;
的所有可能取值构成的集合;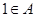 .
.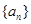 的前
的前 项和为
项和为 ,
,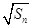 是
是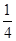 与
与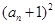 的等比中项.
的等比中项.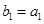 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前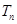 .
. 满足
满足 .
. ,
, ,
, ,
,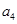 ,由此猜想通项公式
,由此猜想通项公式 ,并用数学归纳法证明此猜想;
,并用数学归纳法证明此猜想; 满足
满足 ,求证:
,求证: .
.