题目内容
数列 ,
,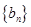 满足
满足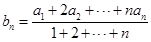
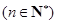 .
.
(1)若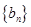 是等差数列,求证:
是等差数列,求证: 为等差数列;
为等差数列;
(2)若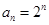 ,求数列
,求数列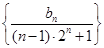 的前
的前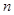 项和
项和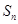 .
.
(1)证明详见解析.(2)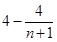 .
.
解析试题分析:(1)由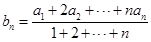 得
得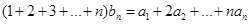 ,
,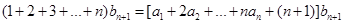 ,相减得
,相减得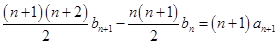 ,再求出
,再求出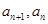 ,最后根据等差数列的定义求证即可.
,最后根据等差数列的定义求证即可.
(2)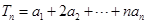 ,利用错位相减法求出数列{Tn}的前n项和,然后求出bn,可得
,利用错位相减法求出数列{Tn}的前n项和,然后求出bn,可得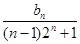
=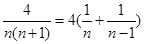 ,最后利用裂项法求出
,最后利用裂项法求出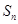 即可.
即可.
试题解析:(1)证明:由题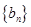 是等差数列,设
是等差数列,设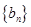 的公差为
的公差为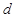
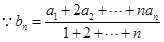
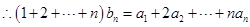 ①;
①;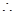 有
有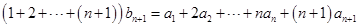 ② 3分
② 3分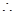 ②-①可得:
②-①可得: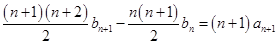
即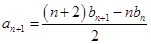
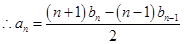 5分
5分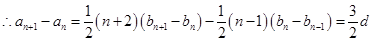
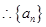 是公差为
是公差为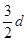 的等差数列 7分
的等差数列 7分
(2)记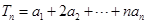 ,
,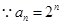
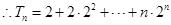 ①
① 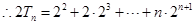 ②
②
①-②得: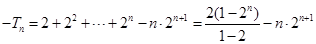
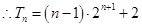 ,
,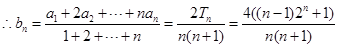 11分
11分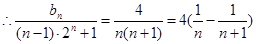 13分
13分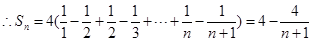 14分
14分
考点:1.数列的递推公式和等差数列的判定;2.数列前n项和的求法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 所表示的平面区域为
所表示的平面区域为 ,记
,记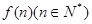
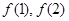 的值及
的值及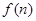 的表达式;
的表达式;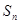 为数列
为数列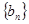 的前
的前 项的和,其中
项的和,其中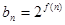 ,问是否存在正整数
,问是否存在正整数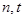 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数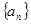 中,
中,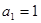 ,
,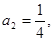 且
且
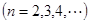 .
.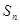 为数列
为数列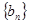 的前
的前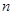 项和,且
项和,且
 .
. ,求数列
,求数列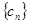 的前
的前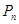 ;
;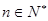 ,有
,有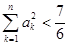 .
.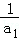 +
+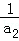 +…+
+…+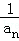 <
<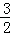 .
.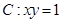 ,过
,过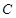 上一点
上一点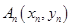 作一斜率为
作一斜率为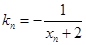 的直线交曲线
的直线交曲线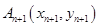 (
(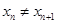 且
且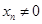 ,点列
,点列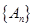 的横坐标构成数列
的横坐标构成数列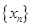 ,其中
,其中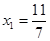 .
.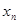 与
与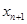 的关系式;
的关系式;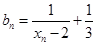 ,求证:数列
,求证:数列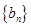 是等比数列;
是等比数列;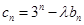 (
( 为非零整数,
为非零整数,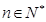 ),试确定
),试确定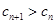 成立.
成立.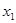 (
( 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为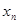 ,该年的增长量
,该年的增长量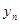 和
和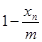 的乘积成正比,比例系数为
的乘积成正比,比例系数为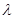
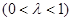 其中
其中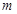 =200万.
=200万.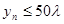 ;
;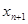 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.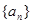 ,
,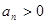 ,
,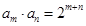 ,
,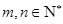 .
.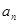 ;
;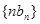 的前
的前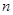 项和为
项和为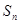 且
且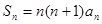 ,求
,求
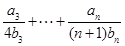 .
.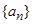 中,
中,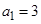 ,前
,前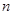 和
和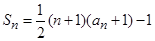
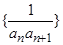 的前
的前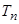 ,是否存在实数
,是否存在实数 ,使得
,使得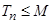 对一切正整数
对一切正整数