题目内容

【题目】已知关于的方程的三个实根分别为一个椭圆，一个抛物线，一个双曲线的离心率，则的取值范围（ ）

A. B.

C. D.

【答案】C

【解析】令f（x）=x3+ax2+bx+c

∵抛物线的离心率为1，∴1是方程f（x）=x3+ax2+bx+c=0的一个实根∴a+b+c=﹣1

∴c=﹣1﹣a﹣b代入f（x）=x3+ax2+bx+c，

可得f（x）=x3+ax2+bx﹣1﹣a﹣b=（x﹣1）（x2+x+1）+a（x+1）（x﹣1）+b（x﹣1）=（x﹣1）

设g（x）=x2+（a+1）x+1+a+b，则g（x）=0的两根满足0＜x1＜1，x2＞1

∴g（0）=1+a+b＞0，g（1）=3+2a+b＜0

作出可行域，如图所示

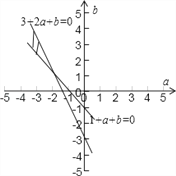
的几何意义是区域内的点与原点连线的斜率，∴故答案为：C

练习册系列答案
相关题目

【题目】已知函数
（1）当a=2时，求f（x）在x∈[0，1]的最大值；
（2）当0＜a＜1，f（x）在x∈[0，1]上的最大值和最小值之和为a，求a的值．

【题目】设等差数列{an}的前n项和为Sn ， 且S4=4S2 ， a2n=2an+1．
（Ⅰ）求数列{an}的通项公式
（Ⅱ）设数列{bn}的前n项和为Tn ， 且 （λ为常数）．令cn=b2n ， （n∈N*），求数列{cn}的前n项和Rn ．

【题目】若二次函数的图象和直线无交点，现有下列结论：

①方程一定没有实数根；②若，则不等式对一切实数都成立；

③若，则必存在实数，使；④若，则不等式对一切实数都成立；⑤函数的图象与直线也一定没有交点，其中正确的结论是__________．(写出所有正确结论的编号)

【题目】已知数列{an}是等比数列，且a2013+a2015= dx，则a2014（a2012+2a2014+a2016）的值为（ ）
A.π2
B.2π
C.π
D.4π2

【题目】已知函数 ，m∈R．
（1）当m=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）若f（x）在区间（﹣2，3）上是减函数，求m的取值范围．

【题目】已知函数f（x）= ．
（1）用定义证明函数f（x）在（﹣∞，+∞）上为减函数；
（2）若x∈[1，2]，求函数f（x）的值域；
（3）若g（x）= ，且当x∈[1，2]时g（x）≥0恒成立，求实数a的取值范围．

【题目】定义在上的偶函数，其导函数为，若对任意的实数，都有恒成立，则使成立的实数的取值范围为（　　）

A. B. （﹣∞，﹣1）∪（1，+∞）

C. （﹣1，1） D. （﹣1，0）∪（0，1）

【题目】已知函数．

（1）试讨论的单调性；

（2）证明：对于正数，存在正数，使得当时，有；

（3）设（1）中的的最大值为，求得最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网