Question

【题目】已知函数f（x）= ．
（1）用定义证明函数f（x）在（﹣∞，+∞）上为减函数；
（2）若x∈[1，2]，求函数f（x）的值域；
（3）若g（x）= ，且当x∈[1，2]时g（x）≥0恒成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：设x1＜x2，

则f（x1）﹣f（x2）= ﹣

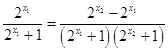
∵x1＜x2，∴2x2﹣2x1＞0

又2x1+1＞0，2x2+1＞0，

f（x1）﹣f（x2）＞0即f（x1）＞f（x2）

∴f（x）在（﹣∞，+∞）上为减函数

（2）解：∵f（x）在（﹣∞，+∞）上为减函数，

∴f（x）值域为

（3）解：当x∈[{1，2}]时，g（x）∈

∵g（x）≥0在x∈[1，2]上恒成立，

∴ ，∴

【解析】（1）根据函数单调性的定义，先在所给区间上任设两个数并确定好大小，然后通过作差法即可获得自变量对应函数值的大小关系，由定义即可获得问题的解答；（2）结合（1）所证明的结论即可获得函数在[1，2]上的单调性，从而可以求的函数在[1，2]上的最值，进而问题即可获得解答；（3）充分利用前两问答结论，即可获得g（x）= 在[1，2]上的最值，结合恒成立的条件即可将问题转化为实数a的不等关系，求解即可获得问题的解答．