题目内容
17.购买8角和2元的邮票若干张,并要求每种邮票至少有两张.若小明带有10元钱,则小明有11种买法.分析 根据题意,设小明买8角的邮票x张,2元的邮票y张,结合题意可得关于x、y的不等式组2≤x≤12,2≤y≤5,且0.8x+2y≤10,在平面区域中表示出来.用列举发找出其区域中整点的个数,即可得答案.
解答  解:根据题意,设小明买8角的邮票x张,2元的邮票y张,
解:根据题意,设小明买8角的邮票x张,2元的邮票y张,
由于小明带有10元钱,则有2≤x≤12,2≤y≤5,且0.8x+2y≤10,
为如图表示的平面区域,
分析可得:当y=2时,x可取的值为2、3、4、5、6、7,共6个值;
当y=3时,x可取的值为2、3、4、5,共4个值;
当y=4时,x可取的值为2,只有一个值;
则在区域内的点有6+4+1=11个,
即小明有11种买法;
故答案为:11.
点评 本题考查线性规划问题的运用,解题的关键是设出未知数,结合题意得到不等式组,转化为线性规划问题求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.二项展开式(2x-1)10中x的奇次幂项的系数之和为( )
| A. | $\frac{1+{3}^{10}}{2}$ | B. | $\frac{1-{3}^{10}}{2}$ | C. | $\frac{{3}^{10}-1}{2}$ | D. | -$\frac{1+{3}^{10}}{2}$ |
12.设x为实数,命题p:?x∈R,x2+x+1≥0的否定是( )
| A. | ¬p:?x0∈R,x02+x0+1<0 | B. | ¬p:?x0∈R,x02+x0+1≤0 | ||
| C. | ¬p:?x0∈R,x02+x0+1<0 | D. | ¬p:?x0∈R,x02+x0+1≤0 |
2.设f(x)=$\left\{\begin{array}{l}{x-3,x≥10}\\{f(x+5),x<10}\end{array}\right.$,则f(6)的值是( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
9.不等式$\frac{{-{x^2}-2x+3}}{x+1}$≥0的解集为( )
| A. | {x|x≥3或-1≤x≤1} | B. | {x|x≥3或-1<x≤1} | C. | {x|x≤-3或-1≤x≤1} | D. | {x|x≤-3或-1<x≤1} |
6.函数f(x)=-x3+ax在[0,+∞)上是减函数,则a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
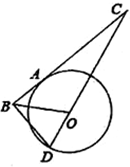 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.