题目内容
【题目】如图，在正方体
中，
平面
，垂足为H，给出下面结论：
①直线
与该正方体各棱所成角相等；
②直线与该正方体各面所成角相等；
③过直线的平面截该正方体所得截面为平行四边形；
④垂直于直线的平面截该正方体，所得截面可能为五边形，
其中正确结论的序号为（ ）
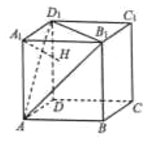
A. ①③ B. ②④ C. ①②④ D. ①②③
【答案】D
【解析】
由A1C⊥平面AB1D1，直线A1H与直线A1C重合，结合线线角和线面角的定义，可判断①②；由四边形A1ACC1为矩形，可判断③；由垂直于直线A1H的平面与平面AB1D1平行，可判断④．
如图，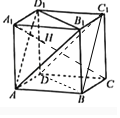
在正方体ABCD﹣A1B1C1D1中，A1H⊥平面AB1D1，垂足为H，
连接A1C，可得A1C⊥AB1，A1C⊥AD1，即有A1C⊥平面AB1D1，
直线A1H与直线A1C重合，
直线A1H与该正方体各棱所成角相等，均为arctan
，故①正确；
直线A1H与该正方体各面所成角相等，均为arctan
，故②正确；
过直线A1H的平面截该正方体所得截面为A1ACC1为平行四边形，故③正确；
垂直于直线A1H的平面与平面AB1D1平行，截该正方体，
所得截面为三角形或六边形，不可能为五边形．故④错误．
故选：D．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
