题目内容
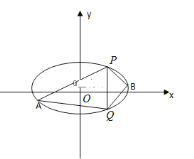
【题目】如图,已知四棱锥P—ABCD,底面ABCD是边长为4的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
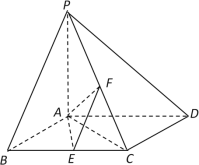
(Ⅰ)求证:AE⊥PD;
(Ⅱ)若PA=4,求二面角E—AF—C的余弦值.
【答案】(Ⅰ)见解析 (Ⅱ)![]() .
.
【解析】
(Ⅰ)通过证明PA⊥AE和AE⊥AD,可证得AE⊥平面PAD,从而得证;
(Ⅱ)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,分别求面AEF和面AFC的法向量,利用法向量求解二面角即可.
(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE![]() 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而PA![]() 平面PAD,AD
平面PAD,AD![]() 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以AE⊥平面PAD,又PD![]() 平面PAD.所以 AE⊥PD.
平面PAD.所以 AE⊥PD.
(Ⅱ)解:由(Ⅰ)知AE、AD、AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2![]() ,—2,0),C(2
,—2,0),C(2![]() ,2,0),D(0,4, 0),P(0,0,4),E(2
,2,0),D(0,4, 0),P(0,0,4),E(2![]() ,0,0),F(
,0,0),F(![]() ),
),
所以![]() =(2
=(2![]() ,0,0),
,0,0),![]() =(
=(![]() )
)
设平面AEF的法向量为![]() =(
=(![]() ),
),
则 ,因此
,因此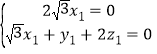
取![]() ,则
,则![]() =(0,2,—1),
=(0,2,—1),
因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故![]() 为平面AFC的法向量.
为平面AFC的法向量.
又![]() (—2
(—2![]() ,6,0),所以cos<
,6,0),所以cos<![]() ,
,![]() >=
>=![]() .
.
因为二面角E—AF—C为锐角,所以所求二面角的余弦值为![]() .
.

【题目】为了解市民对A,B两个品牌共享单车使用情况的满意程度,分别从使用A,B两个品牌单车的市民中随机抽取了100人,对这两个品牌的单车进行评分,满分60分.根据调查,得到A品牌单车评分的频率分布直方图,和B品牌单车评分的频数分布表:


根据用户的评分,定义用户对共享单车评价的“满意度指数”如下:
评分 |
|
|
|
满意度指数 |
|
|
|
(1)求对A品牌单车评价“满意度指数”为![]() 的人数;
的人数;
(2)从对A,B两个品牌单车评分都在![]() 范围内的人中随机选出2人,求2人中恰有1人是A品牌单车的评分人的概率;
范围内的人中随机选出2人,求2人中恰有1人是A品牌单车的评分人的概率;