题目内容
【题目】【2018届天津市耀华中学高三上学期第三次月考】已知椭圆![]() 的一个焦点在直线
的一个焦点在直线![]() 上,且离心率
上,且离心率![]() .
.
(1)求该椭圆的方程;
(2)若![]() 与
与![]() 是该椭圆上不同的两点,且线段
是该椭圆上不同的两点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,试证:
上,试证: ![]() 轴上存在定点
轴上存在定点![]() ,对于所有满足条件的
,对于所有满足条件的![]() 与
与![]() ,恒有
,恒有![]() ;
;
(3)在(2)的条件下, ![]() 能否为等腰直角三角形?并证明你的结论.
能否为等腰直角三角形?并证明你的结论.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析: ![]() 利用椭圆的性质,离心率计算公式
利用椭圆的性质,离心率计算公式![]() 及
及![]() 即可求出;
即可求出;
⑵分直线![]() 的斜率存在与不存在两种情况:
的斜率存在与不存在两种情况: ![]() 斜率存在时,设出其方程,与椭圆方程联立得到关于斜率的方程式,从而得到
斜率存在时,设出其方程,与椭圆方程联立得到关于斜率的方程式,从而得到![]() 坐标间的关系式。假设
坐标间的关系式。假设![]() 轴上存在定点
轴上存在定点![]() ,对于所有满足条件的
,对于所有满足条件的![]() ,恒有
,恒有![]() ,得到点
,得到点![]() 的坐标,即证命题存在;当直线
的坐标,即证命题存在;当直线![]() 的斜率不存在时,易知
的斜率不存在时,易知![]() 成立,命题得证;
成立,命题得证;
⑶分类讨论,利用等腰直角三角形的性质和两点间的距离关系及其根与系数的关系即可得到满足条件的直线斜率![]() 存在即可;
存在即可;
解析:(1)∵椭圆![]() 的一个焦点在直线
的一个焦点在直线![]() 上,∴
上,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴该椭圆的方程为![]() .
.
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
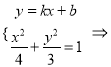
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
∵弦![]() 的中点
的中点![]() 在直线
在直线![]() 上,∴
上,∴![]()
![]() ,
,
∴![]()
![]() ,∴
,∴![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,
,
假设在![]() 轴上存在定点
轴上存在定点![]() ,
, ![]()
![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]()
![]() ,即
,即![]() ,
,
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 垂直于
垂直于![]() 轴,此时
轴,此时![]() 显然成立,综上,
显然成立,综上, ![]() 轴上存在定点
轴上存在定点![]() .
.
(3)假设![]() 能为等腰直角三角形,则
能为等腰直角三角形,则![]() ,
,
∴![]() ,
,
![]() ,
,
![]()
![]() ,
,
又![]() ,
,
∴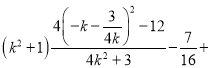
![]() ,
,
![]()
![]() ,符合(*),
,符合(*),
∴在(2)的条件下, ![]() 能为等腰直角三角形.
能为等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目