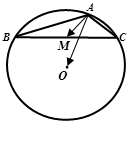题目内容
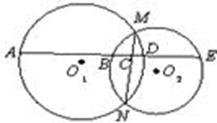
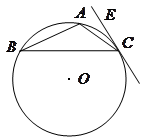
(本题满分12分)如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC。
(1)求证:FB=FC;
(2)若AB是△ABC的外接圆的直径,∠EAC =120°,BC=6,求AD的长。
(1)求证:FB=FC;
(2)若AB是△ABC的外接圆的直径,∠EAC =120°,BC=6,求AD的长。
证明:见解析;(2)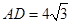 .
.
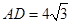 .
.本试题主要是考查了圆内的性质的运用,以及直角三角形中边角关系的综合运用。
(1)因为AD平分∠EAC,所以∠EAD=∠DAC.
因为四边形AFBC内接于圆,所以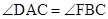 ,所以
,所以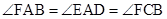 ,
,
所以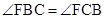 ,所以FB=FC.
,所以FB=FC.
(2)因为AB是△ABC的外接圆的直径,则所对的圆周角为直角,然后利用圆周角定理得到边长。
证明:因为AD平分∠EAC,所以∠EAD=∠DAC.
因为四边形AFBC内接于圆,所以 ,所以
,所以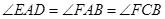 ,
,
所以 ,所以FB=FC.
,所以FB=FC.
(2)解:因为AB是△ABC的外接圆的直径,所以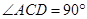 .
.
因为 =
=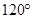 ,所以
,所以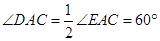 ,
, .
.
在Rt△ACB中,因为BC=6, ,所以
,所以 .
.
又在Rt△ACD中, ,
, ,所以
,所以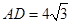 .
.
(1)因为AD平分∠EAC,所以∠EAD=∠DAC.
因为四边形AFBC内接于圆,所以
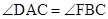 ,所以
,所以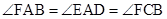 ,
,所以
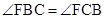 ,所以FB=FC.
,所以FB=FC.(2)因为AB是△ABC的外接圆的直径,则所对的圆周角为直角,然后利用圆周角定理得到边长。
证明:因为AD平分∠EAC,所以∠EAD=∠DAC.
因为四边形AFBC内接于圆,所以
 ,所以
,所以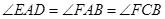 ,
,所以
 ,所以FB=FC.
,所以FB=FC. (2)解:因为AB是△ABC的外接圆的直径,所以
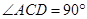 .
. 因为
 =
=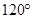 ,所以
,所以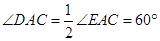 ,
, .
. 在Rt△ACB中,因为BC=6,
 ,所以
,所以 .
. 又在Rt△ACD中,
 ,
, ,所以
,所以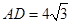 .
.
练习册系列答案
相关题目
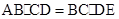
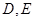 分别为
分别为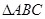 边
边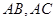 的中点,直线
的中点,直线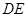 交
交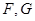 两点,若
两点,若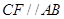 ,证明:
,证明: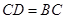 ;
;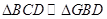
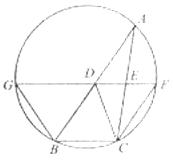
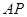 是
是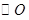 的切线,
的切线,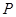 为切点,
为切点,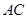 是
是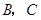 两点,圆心
两点,圆心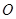 在
在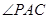 的内部,点
的内部,点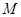 是
是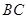 的中点.
的中点.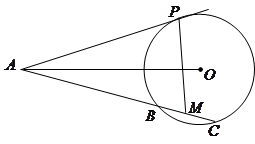
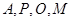 四点共圆;
四点共圆;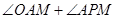 的大小.
的大小.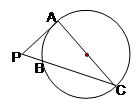
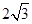 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 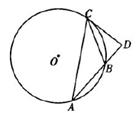
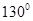 ,则
,则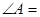 ( )
( )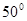
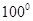
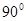
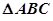 是圆O的内接三角形,圆O的半径
是圆O的内接三角形,圆O的半径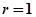 ,
,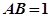 ,
,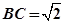 ,
,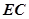 是圆
是圆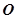 的切线,则
的切线,则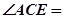 _______.
_______.
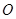 为△
为△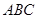 的外心,
的外心,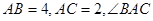 为钝角,
为钝角, 是边
是边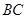 的中点,则
的中点,则 的值 ( ).
的值 ( ).