题目内容
(本小题满分13分)已知抛物线C: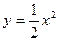 与直线l:
与直线l: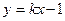 没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
(1)证明:直线AB恒过定点Q;
(2)若点P与(1)中的定点Q的连线交抛物线C于M,N两点,证明: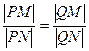 .
.
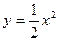 与直线l:
与直线l: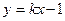 没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.(1)证明:直线AB恒过定点Q;
(2)若点P与(1)中的定点Q的连线交抛物线C于M,N两点,证明:
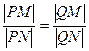 .
.见解析
(1)设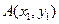 ,则
,则 .
.
由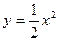 得
得 ,所以
,所以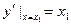 .
.
于是抛物线C在A点处的切线方程为 ,即
,即 .
.
设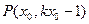 ,则有
,则有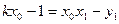 .设
.设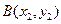 ,同理有
,同理有 .
.
所以AB的方程为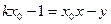 ,即
,即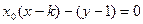 ,所以直线AB恒过定点
,所以直线AB恒过定点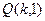 .
.
(2) PQ的方程为 ,与抛物线方程
,与抛物线方程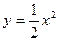 联立,消去y,得
联立,消去y,得
 .
.
设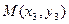 ,
,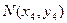 ,则
,则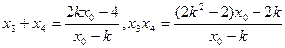 ①
①
要证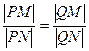 ,只需证明
,只需证明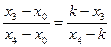 ,即
,即 ②
②
由①知,②式左边=
 .故②式成立,从而结论成立.
.故②式成立,从而结论成立.
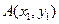 ,则
,则 .
.由
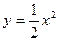 得
得 ,所以
,所以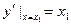 .
.于是抛物线C在A点处的切线方程为
 ,即
,即 .
.设
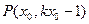 ,则有
,则有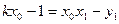 .设
.设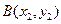 ,同理有
,同理有 .
.所以AB的方程为
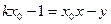 ,即
,即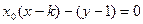 ,所以直线AB恒过定点
,所以直线AB恒过定点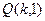 .
.(2) PQ的方程为
 ,与抛物线方程
,与抛物线方程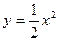 联立,消去y,得
联立,消去y,得 .
.设
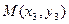 ,
,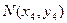 ,则
,则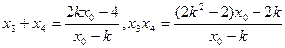 ①
①要证
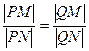 ,只需证明
,只需证明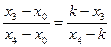 ,即
,即 ②
②由①知,②式左边=

 .故②式成立,从而结论成立.
.故②式成立,从而结论成立. 
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )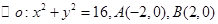 为两定点,
为两定点,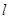 为
为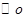 的一条切线,若过
的一条切线,若过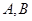 的抛物线以直线
的抛物线以直线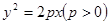 的准线与圆
的准线与圆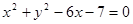 相切,则
相切,则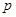 的值为
的值为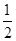
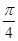 的直线过抛物线
的直线过抛物线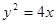 的焦点且与抛物线交于A,B两点,则
的焦点且与抛物线交于A,B两点,则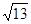
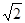
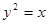 的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角
的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角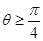 ,则|FA|的取值范围是( )
,则|FA|的取值范围是( )



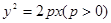 的焦点为
的焦点为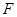 ,
,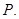 过
过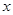 轴的垂线交抛物线于
轴的垂线交抛物线于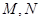 两点.有下列四个命题:①
两点.有下列四个命题:①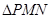 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线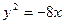 的准线与双曲线
的准线与双曲线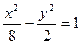 的两条渐近线所围成的三角形的面积为
的两条渐近线所围成的三角形的面积为 B.
B.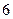 C.
C.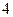 D. 2
D. 2