题目内容
倾斜角为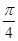 的直线过抛物线
的直线过抛物线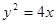 的焦点且与抛物线交于A,B两点,则
的焦点且与抛物线交于A,B两点,则
|AB|= ( )
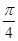 的直线过抛物线
的直线过抛物线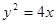 的焦点且与抛物线交于A,B两点,则
的焦点且与抛物线交于A,B两点,则|AB|= ( )
A.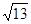 | B.8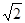 | C.16 | D.8 |
D
分析:求出焦点坐标,点斜式求出直线的方程,代入抛物线的方程利用根与系数的关系,由弦长公式求得|AB|.
解答:解:抛物线y2=4x的焦点即(1,0),倾斜角为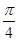 的直线的斜率等于1,故直线的方程为
的直线的斜率等于1,故直线的方程为
y-0=x-1,代入抛物线的方程得 x2-6x+1=0,∴x1+x2=6,x1x2=1,
∴|AB|=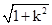 ?|x1-x2|=
?|x1-x2|=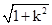 ?
?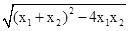 =
=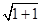 ?
?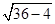 =8,
=8,
故选D.
解答:解:抛物线y2=4x的焦点即(1,0),倾斜角为
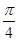 的直线的斜率等于1,故直线的方程为
的直线的斜率等于1,故直线的方程为y-0=x-1,代入抛物线的方程得 x2-6x+1=0,∴x1+x2=6,x1x2=1,
∴|AB|=
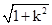 ?|x1-x2|=
?|x1-x2|=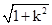 ?
?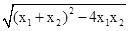 =
=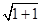 ?
?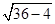 =8,
=8,故选D.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
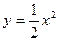 与直线l:
与直线l: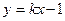 没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.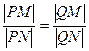 .
.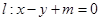 与抛物线
与抛物线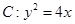 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。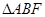 的重心G的轨迹方程;
的重心G的轨迹方程;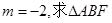 的外接圆的方程。
的外接圆的方程。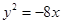 的焦点坐标是 ( )
的焦点坐标是 ( )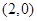 B
B 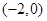 C
C 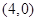 D
D 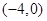
 上,则抛物线的方程为
上,则抛物线的方程为 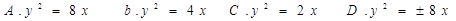
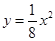 的焦点坐标是 .
的焦点坐标是 .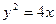 的焦点为F,在第一象限中过抛物线上任意一点P的切线为
的焦点为F,在第一象限中过抛物线上任意一点P的切线为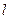 ,过P点作平行于
,过P点作平行于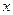 轴的直线
轴的直线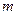 ,过焦点F作平行于
,过焦点F作平行于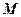 ,若
,若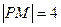 ,则点P的坐标为 .
,则点P的坐标为 .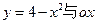 所围成的图形的面积的值是 。
所围成的图形的面积的值是 。