题目内容
(本题满分15分) 已知直线l1:x=my与抛物线C:y2=4x交于O (坐标原点),A两点,直线l2:x=my+m 与抛物线C交于B,D两 点.
点.
(Ⅰ) 若 | BD | = 2 | OA |,求实数m的值;
(Ⅱ) 过A,B,D分别作y轴的垂线,垂足分别为A1,B1,D1.记S1,S2分别为三角形OAA1和四 边形BB1D1D的面积,求
边形BB1D1D的面积,求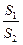 的取值范围.
的取值范围.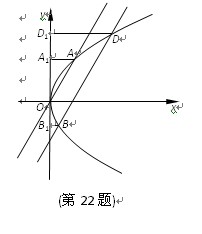
 点.
点. (Ⅰ) 若 | BD | = 2 | OA |,求实数m的值;
(Ⅱ) 过A,B,D分别作y轴的垂线,垂足分别为A1,B1,D1.记S1,S2分别为三角形OAA1和四
 边形BB1D1D的面积,求
边形BB1D1D的面积,求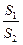 的取值范围.
的取值范围.
(Ⅰ) m=

(Ⅱ)
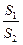 的取值范围是(0,1)∪(1,+∞)
的取值范围是(0,1)∪(1,+∞)(Ⅰ) 解: 设B(x1,y1), D(x2,y2),
由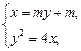 得
得
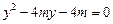 ,
,
由Δ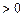 ,得
,得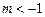 或
或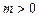 ,
,
且y1+y2=4m, y1y2=-4m.
又由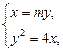 得
得
y2-4my=0,
所以y=0或4m.
故A (4m2,4m).
由 | BD |=2 | OA |,得
(1+m2)(y1-y2)2=4 (16m4+16m2),
而 (y1-y2)2=16m2+16m,
故m= . ………………………… 6分
. ………………………… 6分
(Ⅱ) 解: 由(Ⅰ)得
x1+x2=m(y1+y 2)+2m=4m2+2m.
2)+2m=4m2+2m.
所以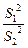 =
=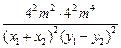
=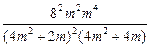
=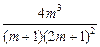
=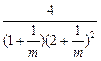 .
.
令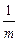 =t,
=t,
因为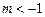 或
或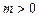 ,
,
所以-1<t<0或t>0.
故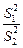 =
=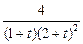 ,
,
所以 0<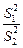 <1 或
<1 或 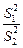 >1,
>1,
即 0<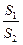 <1 或
<1 或 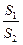 >1.
>1.
所以,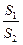 的取值范围是(0,1)∪(1,+∞). ………………………15分
的取值范围是(0,1)∪(1,+∞). ………………………15分
由
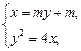 得
得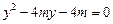 ,
,由Δ
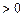 ,得
,得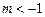 或
或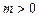 ,
,且y1+y2=4m, y1y2=-4m.
又由
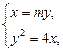 得
得y2-4my=0,
所以y=0或4m.
故A (4m2,4m).
由 | BD |=2 | OA |,得
(1+m2)(y1-y2)2=4 (16m4+16m2),
而 (y1-y2)2=16m2+16m,
故m=
 . ………………………… 6分
. ………………………… 6分(Ⅱ) 解: 由(Ⅰ)得
x1+x2=m(y1+y
 2)+2m=4m2+2m.
2)+2m=4m2+2m.所以
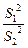 =
=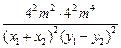
=
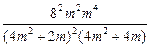
=
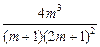
=
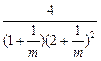 .
.令
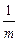 =t,
=t,因为
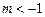 或
或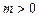 ,
,所以-1<t<0或t>0.
故
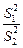 =
=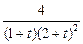 ,
,所以 0<
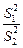 <1 或
<1 或 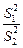 >1,
>1,即 0<
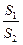 <1 或
<1 或 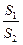 >1.
>1.所以,
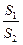 的取值范围是(0,1)∪(1,+∞). ………………………15分
的取值范围是(0,1)∪(1,+∞). ………………………15分
练习册系列答案
相关题目
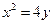 的对称轴上任一点
的对称轴上任一点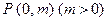 作直线与抛物线交于
作直线与抛物线交于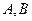 两点,点
两点,点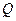 是点
是点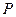 关于原点的对称点.
关于原点的对称点.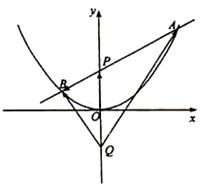
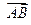 所成的比为
所成的比为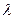 ,证明:
,证明:
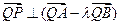 ;
;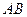 的方程是
的方程是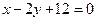 ,过
,过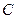 与抛物线在点
与抛物线在点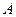 处有共同的切线,求圆
处有共同的切线,求圆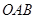 的三个顶点都在抛物线
的三个顶点都在抛物线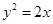 上,其中
上,其中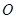 为坐标原点,设圆
为坐标原点,设圆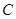 是
是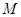 的方程为
的方程为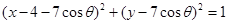 ,过圆
,过圆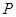 分别作圆
分别作圆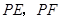 ,切点为
,切点为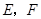 ,求
,求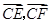 的最大值和最小值.
的最大值和最小值.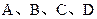 分别为过抛物线
分别为过抛物线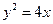 的焦点
的焦点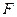 的直线与该抛物线和圆
的直线与该抛物线和圆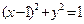 的交点,则
的交点,则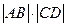 等于 ( )
等于 ( )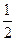

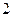
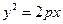 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则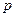 的值为___________
的值为___________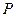 是抛物线
是抛物线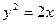 上的一个动点,则点
上的一个动点,则点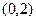 的距离与
的距离与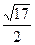
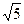
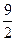
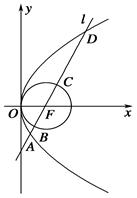
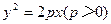 的焦点F的直线
的焦点F的直线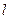 交抛物线于A、B,交其准线于点C,若
交抛物线于A、B,交其准线于点C,若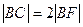 且
且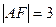 ,则此抛物线的方程为( )
,则此抛物线的方程为( )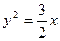 B.
B.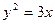 C.
C.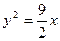 D.
D.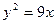
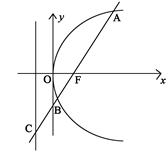
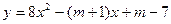 的顶点在
的顶点在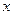 轴上,则
轴上,则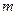 =_________________.
=_________________.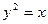 的焦点F,与抛物线相交于A、B两点,且|AB|=3,则线段AB的中点到y轴的距离为( )
的焦点F,与抛物线相交于A、B两点,且|AB|=3,则线段AB的中点到y轴的距离为( )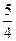 C.
C.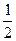 D.2
D.2