题目内容
矩阵M＝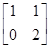
有特征向量为e1＝
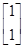，e2＝
，
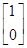(1)求e1和e2对应的特征值；
(2)对向量α＝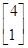
，记作α＝e1＋3e2，利用这一表达式间接计算M4α，M10α.
（1）2，1（2）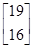
，
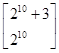
解析
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
作业辅导系列答案同步学典一课多练系列答案经典密卷系列答案金牌课堂练系列答案题目内容
矩阵M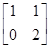＝有特征向量为e1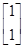＝，e2＝，
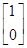(1)求e1和e2对应的特征值；
(2)对向量α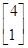＝，记作α＝e1＋3e2，利用这一表达式间接计算M4α，M10α.
（1）2，1（2），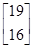
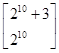
解析
作业辅导系列答案同步学典一课多练系列答案经典密卷系列答案金牌课堂练系列答案
满足
，则行列式
的最小值为 ．
，其中a∈R，若点P(1，－2)在矩阵M的变换下得到点P′(－4，0)，求实数a的值；并求矩阵M的特征值及其对应的特征向量．
的特征值．
，N＝
，在平面直角坐标系中，设直线2x－y＋1＝0在矩阵MN对应的变换作用下得到的曲线F，求曲线F的方程．
对应的变换作用下得到的点的坐标．
．
的逆矩阵
；
的特征值
、
和对应的特征向量
、
．
，且
为纯虚数．
；
，求复数
的模
．
，向量β＝
.求向量α，使得A2α＝β.