题目内容
【题目】小明与另外2名同学进行“手心手背”游戏，规则是：3人同时随机等可能选择手心或手背中的一种手势，规定相同手势人数多者每人得1分，其余每人得0分.现3人共进行了4次游戏，记小明4次游戏得分之和为
，则的期望为（ ）
A.1B.2C.3D.4
【答案】C
【解析】
根据古典概型概率求法,列举出现的所有可能.由离散型随机变量的概率求法,可得小明得分的对应的概率与分布列,即可求出得分之和的期望.
进行“手心手背”游戏,3人出现的所有可能情况如下所示:
(心,心,心), (心,心,背),(心,背,心),(背,心,心)
(心,背,背),(背,心,背),(背,背,心),(背,背,背)
则小明得1分的概率为
,得0分的概率为
进行4次游戏,小明得分共有5种情况:0分,1分,2分,3分,4分
由独立重复试验的概率计算公式可得:
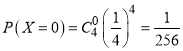
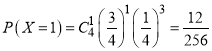
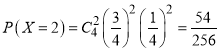
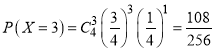
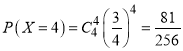
则得分情况的分布列如下表所示:
| 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
则
的期望
故选:C
阅读快车系列答案
【题目】自2017年起，部分省、市陆续实施了新高考，某省采用了“
”的选科模式，即：考试除必考的语、数、外三科外，再从物理、化学、生物、历史、地理、政治六个学科中，任意选取三科参加高考，为了调查新高考中考生的选科情况，某地区调查小组进行了一次调查，研究考生选择化学与选择物理是否有关.已知在调查数据中，选物理的考生与不选物理的考生人数相同，其中选物理且选化学的人数占选物理人数的
，在不选物理的考生中，选化学与不选化学的人数比为
.
（1）若在此次调查中，选物理未选化学的考生有100人，试完成下面的列联表：
选化学 | 不选化学 | 合计（人数） | |
选物理 | |||
不选物理 | |||
合计（人数） |
（2）根据第（1）问的数据，能否有99%把握认为选择化学与选择物理有关？
（3）若研究得到在犯错误概率不超过0.01的前提下，认为选化学与选物理有关，则选物理又选化学的人数至少有多少？（单位：千人；精确到0.001）
附：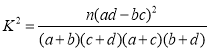
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
