Question

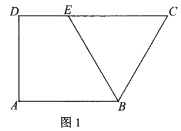
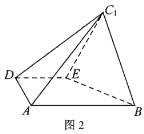
【题目】如图，已知四边形的直角梯形，∥BC，，，，为线段的中点，平面，，为线段上一点（不与端点重合）．

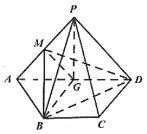
（1）若，

（ⅰ）求证：PC∥平面；

（ⅱ）求平面与平面所成的锐二面角的余弦值；

（2）否存在实数满足，使得直线与平面所成的角的正弦值为，若存在，确定的值，若不存在，请说明理由．

Answer 1

【答案】（1）（ⅰ）证明见解析（ⅱ）（2）存在，

【解析】

（1）（i）连接交于点，连接，，依题意易证四边形为平行四边形，从而有，，由此能证明PC∥平面

（ii）推导出，以为原点建立空间直角坐标系，利用向量法求解；

（2）设，求出平面的法向量，利用向量法求解.

（1）（ⅰ）证明：连接交于点，连接，，

因为为线段的中点，

所以,

因为，所以

因为∥

所以四边形为平行四边形．

所以

又因为，

所以

又因为平面，平面，

所以平面．

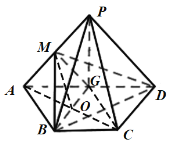
（ⅱ）解：如图，在平行四边形中

因为，，

所以

以为原点建立空间直角坐标系

则，，，

所以，，，

平面的法向量为

设平面的法向量为，

则，即，取，得，

设平面和平面所成的锐二面角为，则

所以锐二面角的余弦值为

（2）设

所以，，

设平面的法向量为，则

，取，得，

因为直线与平面所成的角的正弦值为，

所以

解得

所以存在满足，使得直线与平面所成的角的正弦值为.