题目内容
【题目】已知
(1)求函数
的极值；
(2)设
，对于任意
，总有
成立，求实数
的取值范围.
【答案】(1) 
的极小值为： 
，极大值为： 
(2) 
【解析】试题分析:(1)先求函数的定义域,然后对函数求导,利用导数求得函数的单调区间,进而求得极值.(2)由(1)得到函数
的最大值为
,则只需
.求出函数
的导数,对
分成
两类,讨论函数
的单调区间和最小值,由此求得
的取值范围.
试题解析:
(1) 
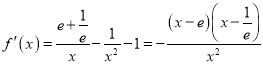
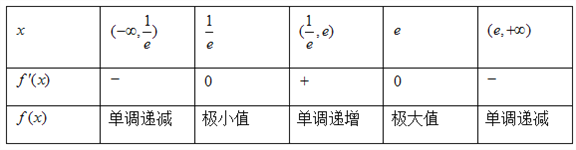
所以
的极小值为： 
，极大值为： 
；
(2) 由(1)可知当
时，函数
的最大值为
对于任意
，总有
成立，等价于
恒成立，
①
时，因为
，所以
，即
在
上单调递增， 
恒成立，符合题意.
②当
时，设
， 
，
所以
在
上单调递增，且
，则存在
，使得
所以
在
上单调递减，在
上单调递增，又
，
所以
不恒成立，不合题意.
综合①②可知，所求实数
的取值范围是
.
练习册系列答案
相关题目
【题目】
年微信用户数量统计显示，微信注册用户数量已经突破
亿．微信用户平均年龄只有
岁， 
的用户在
岁以下， 
的用户在
岁之间，为调查大学生这个微信用户群体中每人拥有微信的数量，现在从北京大学生中随机抽取
位同学进行了抽样调查，结果如下：
微信群数量 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（
）求
， 
， 
的值．
（
）若从
位同学中随机抽取
人，求这
人中恰有
人微信群个数超过
个的概率．
（
）以这
个人的样本数据估计北京市的总体数据且以频率估计概率，若从全市大学生中随机抽取
人，记
表示抽到的是微信群个数超过
个的人数，求
的分布列和数学期望
．
