题目内容
【题目】下列说法中错误的为![]()
A.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]()
B.向量![]() ,
,![]() 不能作为平面内所有向量的一组基底
不能作为平面内所有向量的一组基底
C.若![]() ,则
,则![]() 在
在![]() 方向上的正射影的数量为
方向上的正射影的数量为![]()
D.三个不共线的向量![]() ,
,![]() ,
,![]() ,满足
,满足
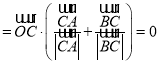 ,则
,则![]() 是
是![]() 的内心
的内心
【答案】AC
【解析】
对于A,由向量的交角为锐角的等价条件为数量积大于0,且两向量不共线,计算即可;
对于B,由![]() ,可知
,可知![]() ,
,![]() 不能作为平面内所有向量的一组基底;
不能作为平面内所有向量的一组基底;
对于C,利用向量投影的定义即可判断;
对于D,由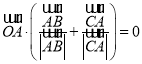 ,点
,点![]() 在角
在角![]() 的平分线上,同理,点
的平分线上,同理,点![]() 在角
在角![]() 的平分线上,点
的平分线上,点![]() 在角
在角![]() 的平分线上,进而得出点
的平分线上,进而得出点![]() 是
是![]() 的内心.
的内心.
对于A,已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,
的夹角为锐角,
可得![]() ,且
,且![]() 与
与![]() 不共线,
不共线,![]() ,
,
即有![]() ,且
,且![]() ,
,
解得![]() 且
且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() 且
且![]() ,
,
故A不正确;
对于B,向量,,![]() ,
,
![]()
![]() ,
,
![]() 向量
向量![]() ,
,![]() 不能作为平面内所有向量的一组基底,故B正确;
不能作为平面内所有向量的一组基底,故B正确;
对于C,若![]() ,则
,则![]() 在
在![]() 上的投影为
上的投影为![]() ,故C错误;
,故C错误;
对于D,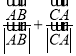 表示与
表示与![]() 中角
中角![]() 的外角平分线共线的向量,
的外角平分线共线的向量,
由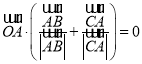 ,可知
,可知![]() 垂直于角
垂直于角![]() 的外角平分线,
的外角平分线,
所以,点![]() 在角
在角![]() 的平分线上,
的平分线上,
同理,点![]() 在角
在角![]() 的平分线上,点
的平分线上,点![]() 在角
在角![]() 的平分线上,
的平分线上,
故点![]() 是
是![]() 的内心,D正确.
的内心,D正确.
故选:AC.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目