题目内容
【题目】已知函数![]() ,
,![]() 分别是定义在
分别是定义在![]() 上的偶函数和奇函数,且
上的偶函数和奇函数,且![]() .
.
(1)求函数![]() ,
,![]() 的解析式;
的解析式;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)设![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,求
的图象有且只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)4;(3)
;(2)4;(3)![]() 或
或![]()
【解析】
(1)用![]() 替换
替换![]() 再利用奇偶性得到
再利用奇偶性得到![]() ,与已知条件联立即可得到函数
,与已知条件联立即可得到函数![]() ,
,![]() 的解析式;
的解析式;
(2)将![]() 代入,换元思想,分离参数,构造函数,求函数最小值,即可得实数
代入,换元思想,分离参数,构造函数,求函数最小值,即可得实数![]() 的最大值;
的最大值;
(3)根据题意,换元后转化为方程![]() 有且只有一个正根,再对
有且只有一个正根,再对![]() 讨论即可得出
讨论即可得出![]() 的取值范围.
的取值范围.
解:(1)![]() ,用
,用![]() 代替
代替![]() 得
得![]() ,
,
则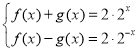 ,
,
解方程得:![]() ,
,![]() .
.
(2)![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,
,![]() ,因为令
,因为令![]() 在
在![]() 单调递增,故
单调递增,故![]()
则![]() 对
对![]() 恒成立
恒成立
当![]() 时,
时,![]() 故
故![]() ,即
,即![]()
(3)由题:方程![]() 有且只有一个根
有且只有一个根
即![]() 有且只有一个根,
有且只有一个根,
令![]() ,因为
,因为![]() 在
在![]() 上单调递增,且
上单调递增,且![]()
故方程![]() (*式)有且只有一个正根
(*式)有且只有一个正根
①当![]() 时,方程有唯一根
时,方程有唯一根![]() ,合题
,合题
②当![]() 时,方程变形为
时,方程变形为![]() ,解得两根为
,解得两根为![]() ,
,![]()
因为(*式)有且只有一个正根,故![]() 或
或![]() ,解得
,解得![]() 或
或![]()
综上:![]() 的取值范围为
的取值范围为![]() 或
或![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目