题目内容
7.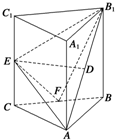 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF.
分析 (1)取AB中点O,连接CO,DO,可证四边形DOCE为平行四边形,从而可得DE∥CO,即可证明DE∥平面ABC.
(2)等腰直角三角形△ABC中F为斜边的中点,连接AF,可证AF⊥BC,又三棱柱ABC-A1B1C1为直三棱柱,可证AF⊥B1F,设AB=AA1=1,由勾股定理可证B1F⊥EF,从而证明B1F⊥平面AEF.
解答 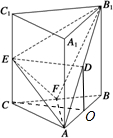 解:(1)证明:取AB中点O,连接CO,DO,
解:(1)证明:取AB中点O,连接CO,DO,
∵DO∥AA1,DO=$\frac{1}{2}$AA1,
∴DO∥CE,DO=CE,
∴四边形DOCE为平行四边形,
∴DE∥CO,DE?平面ABC,CO?平面ABC,
∴DE∥平面ABC.…(5分)
(2)证明:等腰直角三角形△ABC中F为斜边的中点,连接AF,
∴AF⊥BC.…(6分)
又∵三棱柱ABC-A1B1C1为直三棱柱,
∴平面ABC⊥平面BB1C1C,
∴AF⊥平面BB1C1C,
∴AF⊥B1F,…(8分)
设AB=AA1=1,
∴B1F=$\frac{\sqrt{6}}{2}$,EF=$\frac{\sqrt{3}}{2}$,B1E=$\frac{3}{2}$,
∴B1F2+EF2=B1E2,
∴B1F⊥EF,又AF∩EF=F,
∴B1F⊥平面AEF.…(12分)
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知集合A={y|y=x2+2x-3},$B=\left\{{\left.y\right|y=x+\frac{1}{x},x>0}\right\}$,则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=φ |
2.函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是( )
| A. | 2 | B. | $\frac{\sqrt{3}π}{2}$ | C. | $\frac{\sqrt{3}π+3}{3}$ | D. | 1 |
19.已知过点(-2,3)可以作圆(x-a)2+(y-2)2=9的两条切线,则a的范围是( )
| A. | (-∞,-3)∪(3,+∞) | B. | $(-∞,-2-2\sqrt{2})∪(-2+2\sqrt{2},+∞)$ | ||
| C. | (-3,3) | D. | $(-2-2\sqrt{2},-2+2\sqrt{2})$ |
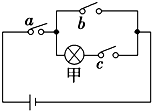 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.