题目内容
1.已知二次函数f(x)=ax2+bx+1和函数g(x)=$\frac{bx-1}{{{a^2}x+2b}}$,且a>0.(1)若g(x)是奇函数,试求f(x)在R上的值域;
(2)若方程g(x)=x有两个不相等的实根,当b>0时,判断f(x)在(-1,1)上的单调性;
(3)若方程g(x)=x的两实根为x1,x2,f(x)=0的两根为x3,x4,求使x3<x1<x2<x4成立的a的取值范围.
分析 (1)根据函数g(x)为奇函数可得b=0,得到f(x)=ax2+1,结合二次函数的性质可得答案;
(2)由方程g(x)=x有两个不相等的实根,可得△=b2-4a2>0,即$\frac{b}{2a}$>1或$\frac{b}{2a}$<-1,再结合二次函数的性质即可判断函数f(x)的单调性;
(3)由题意可得$\left\{\begin{array}{l}{{a}^{2}{x}^{2}+bx+1=0}\\{a{x}^{2}+bx+1=0}\end{array}\right.$,设α为x1与x2中的一个数,则有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{(α-{x}_{3})(α-{x}_{4})<0}\end{array}\right.$,即有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{{α}^{2}+\frac{b}{a}α+\frac{1}{a}<0}\end{array}\right.$.再分a>0与a<0两种情况讨论,进而结合等式与不等式得到关于a的不等式,进而求出a的范围得到答案.
解答 解:(1)因为g(x)为奇函数,
所以g(-x)=-g(x),
又函数g(x)=$\frac{bx-1}{{{a^2}x+2b}}$,
则$\frac{-bx-1}{-{a}^{2}x+2b}$=-$\frac{bx-1}{{{a^2}x+2b}}$,
化简可得b=0,
所以f(x)=ax2+1,定义域为R,
所以函数f(x)的值域为[1,+∞);
(2)由方程g(x)=x整理可得a2x2+bx+1=0,
因为方程g(x)=x有两个不相等的实根,
所以△=b2-4a2>0,即|$\frac{b}{2a}$|>1,即$\frac{b}{2a}$>1或$\frac{b}{2a}$<-1,
又因为函数f(x)=ax2+bx+1的对称轴为x=-$\frac{b}{2a}$,并且a>0,
所以当-$\frac{b}{2a}$<-1时,f(x)在(-1,1)上是增函数;
当-$\frac{b}{2a}$>1时,f(x)在(-1,1)上是减函数.
(3)由$\left\{\begin{array}{l}{g(x)=x}\\{f(x)=0}\end{array}\right.$可得$\left\{\begin{array}{l}{{a}^{2}{x}^{2}+bx+1=0}\\{a{x}^{2}+bx+1=0}\end{array}\right.$,
设α为x1与x2中的一个数,
则有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{(α-{x}_{3})(α-{x}_{4})<0}\end{array}\right.$,
因为x3+x4=-$\frac{b}{a}$,x3x4=$\frac{1}{a}$,
所以有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{{α}^{2}+\frac{b}{a}α+\frac{1}{a}<0}\end{array}\right.$.
当a>0时有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{a{α}^{2}+bα+1<0}\end{array}\right.$,
所以结合两式可得(a-a2)α2<0,
解得:a>1或a<0(舍去).
当a<0时有$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{a{α}^{2}+bα+1>0}\end{array}\right.$,
所以所以结合两式可得(a-a2)α2>0,
解得:0<a<1(舍去).
综上可得a的取值范围为(1,+∞).
点评 本题主要考查函数的奇偶性与函数的单调性,以及一元二次方程的根的分布与系数的关系,此题综合性比较强,考查了数学上一个重要的思想方法即分类讨论的思想方法,此题属于难题.

| A. | $\frac{3\sqrt{5}}{5}$-1 | B. | 1 | C. | 2 | D. | $\frac{3\sqrt{5}}{5}$ |
| A. | 4 | B. | 1 | C. | 0 | D. | -$\frac{4}{3}$ |
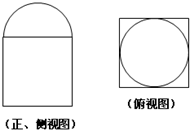 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )| A. | 8+$\frac{2}{3}$π | B. | 8+$\frac{4}{3}$π | C. | 24+π | D. | 20+2π |
| A. | $\frac{3\sqrt{5}}{10}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{5}}{20}$ | D. | $\frac{7\sqrt{5}}{10}$ |
 如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:
如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率: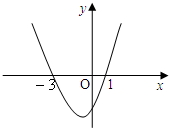 设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.
设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.