题目内容
17. 如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:
如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:(1)在底边BC上任取一点P,使BP<AB;
(2)在∠BAC的内部任作射线AP交线段BC于点P,使BP<AB.
分析 (1)根据几何概型的概率求法,只要求出满足BP<AB的对应线段长度,利用长度比即可;
(2)在∠BAC的内部任作射线AP交线段BC于点P,使BP<AB对于的部分是角度,所以利用角度比求概率.
解答 解:(1)在等腰三角形ABC中,设AB长为1,则BC长为$\sqrt{3}$,
在BC上取点C′,使BC′=1,满足条件BP<1,则P点在线段BC'上,
由几何概型的公式得到在底边BC上任取一点P,使BP<AB的概率为:$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$;
(2)在BC上取BC′=AB,则∠BAC′=$\frac{180°-30°}{2}=75°$.
则所有可能结果的区域为∠BAC,而使BP<AB成立的可能结果区域为∠BAC′.
∵∠BAC=120°,∠BAC'=75°,由几何概型的公式得到,
∠BAC的内部任作射线AP交线段BC于点P使BP<AB的概率为$\frac{75°}{120°}$=$\frac{5}{8}$.
点评 本题给出等腰△ABC,求在两种取法下使得BP<AB的概率.着重考查了几何概型及其应用的知识,属于中档题.解题时注意题意中的“测度”,准确把握“测度”是解决问题的关键.

练习册系列答案
相关题目
6.已知函数y=2cos(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )
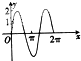

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |