题目内容
11.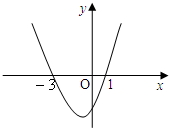 设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.
设f(x)=ax3+bx2+cx的极小值是-5,其导函数的图象如图所示.(1)求f(x)的解析式;
(2)若对任意的x∈[-4,4]都有f(x)≥m2-6m恒成立,求实数m的取值范围.
分析 (1)先求出函数的导数,结合图象得到方程组,解出a,b,c的值即可;
(2)先求出函数f(x)的导数,得到函数的单调区间,从而求出函数的最小值,得到关于m的不等式,求出m的范围即可.
解答 解:(1)因为 f′(x)=3ax2+2bx+c,
由题意,$\left\{\begin{array}{l}f'({-3})=0\\ f'(1)=0\\ f(1)=-5\end{array}\right.$即$\left\{\begin{array}{l}27a-6b+c=0\\ 3a+2b+c=0\\ a+b+c=-5\end{array}\right.$,
解得a=1,b=3,c=-9,
∴f(x)=x3+3x2-9x;
(2)由(1)得:f′(x)=3x2+6x-9,
由图可知,函数在[-4,-3]单调递增,在[-3,1]单调递减,在[1,4]单调递增,
故fmin(x)=f(-4)或f(1),
因为 f(-4)=20,f(1)=-5,故fmin(x)=f(1)=-5,
对任意的x∈[-4,4]都有f(x)≥m2-6m恒成立,
等价为${f_{min}}(x)=-5≥{m^2}-6m$,
解得m∈[1,5].
点评 本题考查了求函数的解析式问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
19.在等腰直角三角形ABC中,角C为直角.在∠ACB内部任意作一条射线CM,与线段AB交于点M,则AM<AC的概率( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
6.已知函数y=2cos(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )
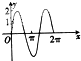

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
20.若关于x的不等式|2x-1|≥|1+a|-|2-a|对任意实数a恒成立,则x的取值范围是( )
| A. | (-∞,0]∪[1,+∞) | B. | [0,1] | C. | (-∞,-1]∪[2,+∞) | D. | [-1,2] |
1.为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,则认为“喜欢乡村音乐与性别有关系”的把握性约为99%
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |