题目内容
11.下列四个结论正确的序号是②③.(填上所有正确的序号)①函数y=xsinx在区间(0,π)内无最大值;
②数列{an}的前n项和Sn=2n(n∈N*),对任意的正整数n总存在正整数m,使得 Sn=am;
③若方程$\frac{{|{sinx}|}}{x}$=k(k>0)有且仅有两个不同的实数根x1,x2(x2>x1),则sinx1+x1cosx2=0.
分析 ①在(0,π)上通过研究单调性的变化即可获得问题的解答;
②利用“当n≥2时,an=Sn-Sn-1,当n=1时,a1=S1”即可得到an,即可得出结论;
③通过数形结合即得结论.
解答 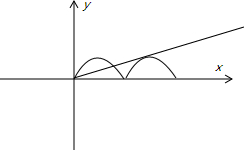 解:①∵y=xsinx,∴y′=sinx+xcosx=$\sqrt{1+{x}^{2}}$sinx(x+θ),其中tanθ=x,
解:①∵y=xsinx,∴y′=sinx+xcosx=$\sqrt{1+{x}^{2}}$sinx(x+θ),其中tanθ=x,
∴存在x=x0使得y′=0,
易得当0<x<x0时,y′>0;当x0<x<π时,y′<0;
故函数y=xsinx在区间(0,π)内存在最大值,故①不正确;
②∵数列{an}的前n项和Sn=2n(n∈N*),
∴当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1;当n=1时,a1=S1=2;
∴an=$\left\{\begin{array}{l}{2,}&{n=1}\\{{2}^{n-1},}&{n≥2}\end{array}\right.$,
∴对任意的正整数n总存在正整数m,使得 Sn=am,故②正确;
③依题意可知x>0,令y1=|sinx|,y2=kx,如图.
∵原方程有且只有两个解,
∴所以y2与y1仅有两个交点,
且第二个交点是y1和y2相切的点,即点(x2,|sinx2|)为切点,
∵(-sinx2)′=-cosx2,∴切线的斜率k=-cosx2,
而且点(x1,sinx1)在切线y2=kx=-cosx2x上,
于是将点(x1,sinx1)代入切线方程y2=xcosx2,可得:sinx1=-x1cosx2,故③正确;
故答案为:②③.
点评 本题考查函数的最值、数列的通项及求和、函数的交点问题,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.椭圆的一焦点与两顶点为等边三角形的三个顶点,则椭圆的长轴长是短轴长的( )
| A. | $\sqrt{3}$倍 | B. | 2倍 | C. | $\sqrt{2}$倍 | D. | $\frac{3}{2}$倍 |
19.已知周长为16的△ABC的两顶点与椭圆M的两个焦点重合,另一个顶点恰好在椭圆M上,则下列椭圆中符合椭圆M条件的是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 |
6. 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )| A. | $\sqrt{5}$+$\sqrt{6}$ | B. | 2$\sqrt{5}$+2$\sqrt{6}$ | C. | $\sqrt{5}$+$\frac{{\sqrt{6}}}{2}$ | D. | 2$\sqrt{5}$+$\sqrt{6}$ |
3.已知点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,则(a-m)2+(b-n)2的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |