题目内容
6.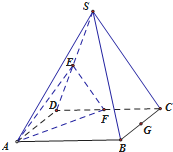 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )| A. | $\sqrt{5}$+$\sqrt{6}$ | B. | 2$\sqrt{5}$+2$\sqrt{6}$ | C. | $\sqrt{5}$+$\frac{{\sqrt{6}}}{2}$ | D. | 2$\sqrt{5}$+$\sqrt{6}$ |
分析 先想着找到P点的轨迹:取SB的中点M,并连接GM,作GN∥AF,与AB交于N,再连接MN,从而可说明平面MNG∥平面AEF,从而便找到P点的轨迹为MG,NG,MN三条线段,把这三线段的长度求出即可.连接AC,BD,并交于O点,连接SO,这样即可分别以OB,OC,OS三直线为x,y,z轴,建立空间直角坐标系,根据条件求出M,N,G三点的坐标,然后利用空间中两点间的距离公式求三线段MG,NG,MN即可.
解答 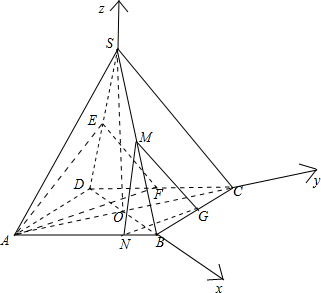 解:取SB中点M,连接GM,则GM∥SC,又EF∥SC;
解:取SB中点M,连接GM,则GM∥SC,又EF∥SC;
∴GM∥EF,EF?平面AEF,GM?平面AEF;
∴GM∥平面AEF;
过G作GN∥AF,交AB于N,并连接GN,同理可得GN∥平面AEF,GM∩GN=G;
∴平面GMN∥平面AEF;
∴动点P的轨迹便是线段MN,MG,NG,轨迹的周长便是MN+MG+NG;
连接AC,BD,并交于O,则分别以OB,OC,OS三直线为x,y,z轴,建立如图所示空间直角坐标系,则:
B($2\sqrt{2}$,0,0),C(0,$2\sqrt{2}$,0),G($\sqrt{2},\sqrt{2},0$),S(0,0,4),M$(\sqrt{2},0,2)$,A(0,-$2\sqrt{2}$,0),N($\frac{3\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$,0);
∴$|MN|=\sqrt{\frac{1}{2}+\frac{1}{2}+4}=\sqrt{5}$,$|MG|=\sqrt{6}$,|NG|=$\sqrt{\frac{1}{2}+\frac{9}{2}}=\sqrt{5}$;
∴P点轨迹的周长为$2\sqrt{5}+\sqrt{6}$.
故选:D.
点评 考查三角形中位线的性质,线面平行的判定定理,面面平行的判定定理,面面平行的性质,以及通过建立空间直角坐标系,利用空间两点间距离公式求空间线段长度的方法,理解轨迹的概念.

 阅读快车系列答案
阅读快车系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{5}{9}$ |
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |