题目内容
16．已知x与y之间的一组数据（如下表），y与x的线性回归直线为$\widehaty=bx+a$，则a-b=-1．| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
分析 求出回归直线方程，即可可得答案．
解答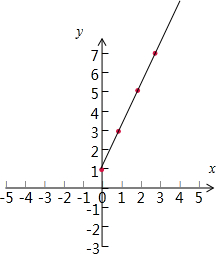 
解：由题意可知，四个点的坐标恰好在一条直线上，直线的斜率为：2，直线方程为：y=2x+1，
∴b=2，a=1，
a-b=-1．
故答案为：-1．
点评 本题考查了回归直线方程的求法，注意本题回归直线的特征是解题的关键．．
练习册系列答案
相关题目
7．已知椭圆C1的方程为：$\frac{x^2}{169}+\frac{y^2}{144}=1$，若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8，则曲线C2的标准方程为（ ）
| A． | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B． | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C． | $\frac{x^2}{169}-\frac{y^2}{25}=1$ | D． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
4．椭圆$\frac{x^2}{2}+{y^2}=1$的离心率等于（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 2 |
1．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点P（3，1），其左、右焦点分别为F1、F2，且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=-6，则椭圆E的离心率是（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{2\sqrt{2}}{3}$ |
已知集合A={x|1＜x＜4}，集合B={x|x＞a}，如图中阴影部分表示的集合是C={x|2＜x＜4}，则a的值为（ ）