题目内容
19.已知周长为16的△ABC的两顶点与椭圆M的两个焦点重合,另一个顶点恰好在椭圆M上,则下列椭圆中符合椭圆M条件的是( )| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 |
分析 设△ABC的两顶点A,B与椭圆的两焦点重合,顶点C在椭圆上,运用椭圆的定义可得|AB|+|AC|+|BC|=2c+2a=16,对选项一一加以判断,即可得到答案.
解答 解:设△ABC的两顶点A,B与椭圆的两焦点重合,顶点C在椭圆上,
由题意可得|AB|+|AC|+|BC|=2c+2a=16,
对于A,a=5,b=4,c=3,即有|AB|+|AC|+|BC|=2×3+2×5=16,满足条件,则A成立;
对于B,a=5,b=3,c=4,即有|AB|+|AC|+|BC|=2×4+2×5=18≠16,不满足条件,则B不成立;
对于C,a=4,b=3,c=$\sqrt{7}$,即有|AB|+|AC|+|BC|=2×$\sqrt{7}$+2×4≠16,不满足条件,则C不成立;
对于D,a=3,b=2,c=$\sqrt{5}$,即有|AB|+|AC|+|BC|=2×$\sqrt{5}$+2×3≠16,不满足条件,则D不成立.
故选:A.
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆的定义的运用,考查运算能力,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
7.已知椭圆C1的方程为:$\frac{x^2}{169}+\frac{y^2}{144}=1$,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{169}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
14.已知曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和ax+by+1=0(ab≠0),在同一坐标系中它们的图形可能是( )
| A. | 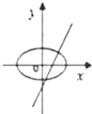 | B. | 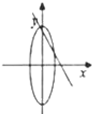 | C. | 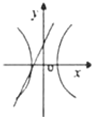 | D. | 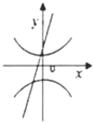 |
4.椭圆$\frac{x^2}{2}+{y^2}=1$的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
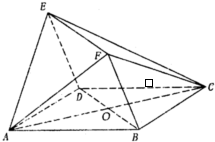 如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.AC与BD相交于O.
如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.AC与BD相交于O.