题目内容
3.已知点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,则(a-m)2+(b-n)2的最小值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |
分析 (a-m)2+(b-n)2的几何意义是y=-x2+3lnx的图象上的点与y=x+2的图象上的点的距离的平方;从而求导,求出切线,求平行线间的距离即可.
解答 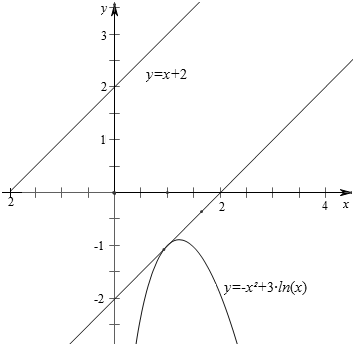 解:∵点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,
解:∵点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,
又∵(a-m)2+(b-n)2的几何意义是点A(a,b)与点B(m,n)两点间距离的平方;
∴(a-m)2+(b-n)2的几何意义是y=-x2+3lnx的图象上的点与y=x+2的图象上的点的距离的平方;
∵y=-x2+3lnx,
∴y′=-2x+3$\frac{1}{x}$=$\frac{3-2{x}^{2}}{x}$,(x>0)
故ymax=-$\frac{3}{2}$+$\frac{3}{2}$ln$\frac{3}{2}$<0,
故y=-x2+3lnx的图象始终在y=x+2的图象的下方,
令y′=-2x+3$\frac{1}{x}$=1得,
x=1;
此时y=-1+0=-1,
故切线方程为y=x-2;
y=x-1与y=x+2的距离为$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$;
故(a-m)2+(b-n)2的最小值为(2$\sqrt{2}$)2=8,
故选D.
点评 本题考查了导数的综合应用及转化的思想应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.已知曲线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和ax+by+1=0(ab≠0),在同一坐标系中它们的图形可能是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知直线l:3x+4y+3=0和圆C:x2+y2-2x-2y+1=0.
(Ⅰ)判断直线l与圆C的位置关系;
(Ⅱ)若P是直线l上的动点,PA是圆C的一条切线,A是切点,求三角形PAC的面积S的最小值.
(Ⅰ)判断直线l与圆C的位置关系;
(Ⅱ)若P是直线l上的动点,PA是圆C的一条切线,A是切点,求三角形PAC的面积S的最小值.
15.若F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,A为双曲线的左顶点,以F1,F2为直径的圆交双曲线的一条渐近线于M,N两点,且满足∠MAN=120°,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
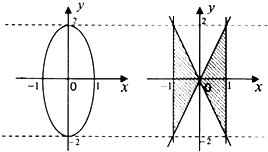 我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.
我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.