题目内容
14.已知O为△ABC的外接圆圆心,AB=2a,AC=$\frac{2}{a}$,∠BAC=120°,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则3x+6y的最小值为6+2$\sqrt{2}$.分析 如图所示,过点O分别作OD⊥AB,OE⊥AC,其垂足分别为D,E,则D,E分别为弦AB,AC的中点.由于AB=2a,AC=$\frac{2}{a}$,∠BAC=120°,可得$\overrightarrow{AB}•\overrightarrow{AC}$=-2.由于$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,可得$\overrightarrow{AO}•\overrightarrow{AB}$=x$\overrightarrow{AB}$$•\overrightarrow{AB}$+y$\overrightarrow{AC}$$•\overrightarrow{AB}$,化为a2=2a2x-2y.同理由$\overrightarrow{AO}•\overrightarrow{AC}$=$x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}$可得:1=-a2x+2y,联立解出x,y,再利用基本不等式的性质即可得出.
解答 解:如图所示,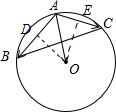
过点O分别作OD⊥AB,OE⊥AC,其垂足分别为D,E,
则D,E分别为弦AB,AC的中点.
∵AB=2a,AC=$\frac{2}{a}$,∠BAC=120°,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=$|2a|•|\frac{2}{a}|cos12{0}^{°}$=-2,
∵$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,
∴$\overrightarrow{AO}•\overrightarrow{AB}$=x$\overrightarrow{AB}$$•\overrightarrow{AB}$+y$\overrightarrow{AC}$$•\overrightarrow{AB}$,
∴$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$x{\overrightarrow{AB}}^{2}$-2y,
∴$\frac{1}{2}(2a)^{2}=x(2a)^{2}$-2y,
化为a2=2a2x-y.
同理由$\overrightarrow{AO}•\overrightarrow{AC}$=$x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}$可得:1=-a2x+2y,
联立$\left\{\begin{array}{l}{2{a}^{2}x-y={a}^{2}}\\{{a}^{2}x-2y=-1}\end{array}\right.$,解得x=$\frac{2{a}^{2}+1}{3{a}^{2}}$,y=$\frac{{a}^{2}+2}{3}$.
∴3x+6y=$\frac{2{a}^{2}+1}{{a}^{2}}$+2a2+4=6+$\frac{1}{{a}^{2}}$+2a2≥6+2$\sqrt{\frac{1}{{a}^{2}}•2{a}^{2}}$=6+2$\sqrt{2}$,当且仅当a2=$\frac{\sqrt{2}}{2}$时取等号.
∴3x+6y的最小值为为6+2$\sqrt{2}$.
故答案为:6+2$\sqrt{2}$.
点评 本题考查了向量的数量积运算性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | 若α⊥β,α∩β=m,m⊥n,则n⊥α,n⊥β | |
| B. | 若α∥β,α∩γ=m,β∩γ=n,则m∥n | |
| C. | 若m不垂直于α,则m不可能垂直于α内的无数条直线 | |
| D. | 若α∩β=m,n∥m,则n∥α,且n∥β |
 如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.AC与BD相交于O.
如图所示的几何体中,四边形ABCD与DBFE均为菱形,∠DAB=∠DBF=60°,且FA=FC.AC与BD相交于O.