题目内容
11.若在平面直角坐标系中,已知动点M和两个定点F1(-$\sqrt{2}$,0),F2($\sqrt{2}$,0),且|MF1|+|MF2|=4(1)求动点M轨迹C的方程;
(2)设O为坐标原点,若点E在轨迹C上,点F在直线y=-2上,且OE⊥OF,试判断直线EF与圆x2+y2=2的位置关系,并说明理由.
分析 (1)由椭圆的定义可求得动点M运动的轨迹.
(2)先由OE⊥OF,所以$\overrightarrow{OE}•\overrightarrow{OF}=0$,讨论直线EF的斜率存在和不存在分别证明直线EF与圆x2+y2=1相切.
解答 解:(1)由题意知:|MF1|+|MF2|=4>|F1F2|=2$\sqrt{2}$
所以,由椭圆的定义可知:动点M运动的轨迹是:以F1,F2为焦点,长轴长为4,焦距为2$\sqrt{2}$的椭圆,且短半轴长为$\sqrt{{2}^{2}-(\sqrt{2})^{2}}=\sqrt{2}$
所以轨迹C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$-----(4分)
(2)直线EF与圆x2+y2=1相切.
证明如下:设E(m,n),F(t,2),显然其中m≠0,
因为OE⊥OF,所以$\overrightarrow{OE}•\overrightarrow{OF}=0$,即tm-2n=0,所以t=$\frac{2n}{m}$
①若直线EF的斜率不存在时,即m=t时,n=$\frac{{t}^{2}}{2}$,代入椭圆方程可得:
${t}^{2}+2×(\frac{{t}^{2}}{2})^{2}=4$,解得:t=$±\sqrt{2}$,
此时直线EF的方程为x=$\sqrt{2}$或x=-$\sqrt{2}$,显然与圆x2+y2=2相切.
②当直线EF的斜率存在,即m≠t时,直线EF的方程为:
y+2=$\frac{n+2}{m-t}(x-t)$,即(n+2)x-(m-t)y-2m-tn=0…(9分)
此时,圆心O(0,0)到直线EF的距离d=$\frac{|-2m-tn|}{\sqrt{(n+2)^{2}+(m-t)^{2}}}$
又因为m2+2n2=4,t=$\frac{2n}{m}$
所以d=$\frac{|2m+tn|}{\sqrt{(n+2)^{2}+(m-t)^{2}}}$=$\frac{|2m+(\frac{2n}{m})×n|}{\sqrt{{m}^{2}+{n}^{2}+4n-2m×(\frac{2n}{m})+4+(\frac{2n}{m})^{2}}}$
=$\frac{|\frac{2{m}^{2}+2{n}^{2}}{m}|}{\sqrt{{m}^{2}+{n}^{2}+\frac{4{n}^{2}}{{m}^{2}}+4}}$=$\frac{|\frac{2{m}^{2}+4-{m}^{2}}{m}|}{\sqrt{{m}^{2}+\frac{4-{m}^{2}}{2}+\frac{8-2{m}^{2}}{{m}^{2}}+4}}$
=$\frac{|\frac{{m}^{2}+4}{m}|}{\sqrt{\frac{{m}^{4}+8{m}^{2}+16}{2{m}^{2}}}}=\sqrt{2}$,所以,直线EF与圆x2+y2=2相切.
综上,直线EF与圆x2+y2=2相切..…(14分)
点评 本题主要考查轨迹方程的求法和利用直线和圆锥曲线的综合问题来证明相切,属于中档题,在高考中属常考题型.

| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
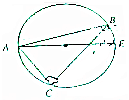 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.