题目内容

4．由曲线y=ex，y=e-x及直线y=e2所围平面区域的面积为（　　）
A．2（e2+1）B．e2-1C．e2+1D．2（e2-1）

分析 由题意，画出所围成的平面区域的图形，利用定积分表示面积，然后计算．

解答 解：由曲线y=ex，y=e-x及直线y=e2所围平面区域如图，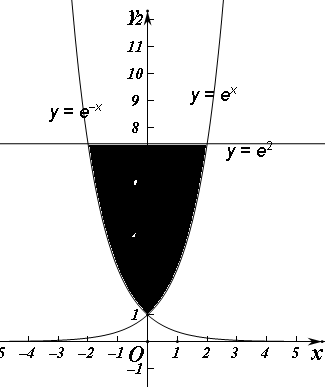
面积为2${∫}_{0}^{2}（{e}^{2}-{e}^{x}）dx$=2（e2x-ex）|${\;}_{0}^{2}$=2（2e2-e2+1）=2（e2+1）；
故选A．

点评 本题考查了利用定积分求曲边梯形的面积，关键是正确利用定积分表示，然后计算定积分．

练习册系列答案
相关题目
14．已知集合A=（2，5]，B=（-∞，a），若A∩B=∅，则实数a的取值范围是（-∞，2]．
15．设集合A={-1，1}，用适当的符号表示集合A与下列集合的关系；
（1）B={x|x∈A}；
（2）C={（x，y）|x，y∈A}；
（3）D={x|x⊆A}．
12．等差数列{an}中，am+n=α，am-n=β，则其公差d的值为$\frac{α-β}{2n}$．
19．已知集合M={x|x=1+a2，a∈N+}，P={x|x=a2+4a+5，a∈N+}，则M与P的关系最确切的是（　　）
A．M⊆PB．M?PC．P⊆MD．P?M
9．下列集合A到集合B的对应f中：
①A={-1，0，1}，B={-1，0，1}，f：A中的数平方；
②A={0，1}，B={-1，0，1}，f：A中的数开方；
③A=Z，B=Q，f：A中的数取倒数；
④A=R，B={正实数}，f：A中的数取绝对值．
是从集合A到集合B的函数为①．
16．已知x∈R，集合A={2，4，x2-5x+9}，若A={2，3，4}，求x的值．
13．解不等式loga（3x+1）＞loga（-2x）（a＞0且a≠1）
14．在下列说法中，错误的是（　　）
A．若平面α内的一条直线垂直于平面β内的任一直线，则α⊥β
B．若平面α内任意一条直线平行于平面β，则α∥β
C．若直线m∥平面α，直线n⊥平面β且α⊥β，则m∥n
D．若平面α∥平面β，任取直线l?α，则l∥β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网