题目内容
14.已知f(x)=ex-x,求过原点与f(x)相切的直线方程y=(e-1)x.分析 根据函数f(x)的解析式设出切点的坐标,根据设出的切点坐标和原点求出切线的斜率,同时由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,两次求出的斜率相等列出关于a的方程,求出方程的解即可得到a的值,进而得到切点坐标,根据切点坐标和切线过原点写出切线方程即可.
解答 解:设切点坐标为(a,ea-a),又切线过(0,0),得到切线的斜率k=$\frac{{e}^{a}-a}{a}$,
又f′(x)=ex-1,把x=a代入得:斜率k=f′(a)=ea-1,则ea-1=$\frac{{e}^{a}-a}{a}$,由于ea>0,则得到a=1,
即切点坐标为(1,e-1),
所以切线方程为:y-e+1=(e-1)(x-1).即y=(e-1)x.
故答案为:y=(e-1)x
点评 此题考查学生会利用导数求曲线上过某点切线方程,注意要区别在某点处的切线,解题的关键是确定切点,本题是一道中档题.

练习册系列答案
相关题目
9.若$\frac{1}{27}$≤x≤9,则f(x)=log3$\frac{x}{27}$•log3(3x)( )
| A. | 有最小值-$\frac{32}{9}$,最大值-3 | B. | 有最小-4,最大值12 | ||
| C. | 有最小值-$\frac{32}{9}$,无最大值 | D. | 无最小值,有最大值12 |
6.已知向量$\overrightarrow a=(cosθ,sinθ)$,向量$\overrightarrow b=(\sqrt{3},-1)$,则|2$\overrightarrow a-\overrightarrow b|$的最大值,最小值分别是( )
| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
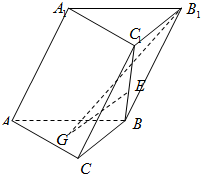 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且$BE=\frac{1}{3}B{C_1}$.
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且$BE=\frac{1}{3}B{C_1}$.