题目内容
19.将y=2cos($\frac{x}{3}$+$\frac{π}{6}$)图象按向量$\overrightarrow{a}$=(-$\frac{π}{4}$,-2)平移,则平移后所得函数的周期及图象的一个对称中心分别为( )| A. | 3π,$({\frac{π}{4},-2})$ | B. | 6π,$({\frac{3π}{4},2})$ | C. | 6π,$({\frac{3π}{4},-2})$ | D. | 3π,$({\frac{π}{4},2})$ |
分析 直接利用函数图象的平移否则,即可求出平移后的函数解析式.利用周期公式可求函数的周期,利用$\frac{x}{3}$+$\frac{π}{4}$=k$π+\frac{π}{2}$(k∈Z)可解得图象的一个对称中心.
解答 解:将y=2cos($\frac{x}{3}$+$\frac{π}{6}$)图象按向量$\overrightarrow{a}$=(-$\frac{π}{4}$,-2)平移,得到函数y=2cos[$\frac{1}{3}$(x+$\frac{π}{4}$)+$\frac{π}{6}$]-2的图象,
即函数y=2cos($\frac{x}{3}$+$\frac{π}{4}$)-2的图象.
所以函数的周期T=$\frac{2π}{\frac{1}{3}}$=6π,
由:$\frac{x}{3}$+$\frac{π}{4}$=k$π+\frac{π}{2}$(k∈Z)可解得图象的一个对称中心为:(3kπ$+\frac{3π}{4}$,-2)k∈Z,
当k=0时,有图象的一个对称中心为:($\frac{3π}{4}$,-2)k∈Z,
故选:C.
点评 本题主要考查了向量的平移,函数解析式的求法,注意向量的平移和函数图象的平移的区别,属于基本知识的考查.

练习册系列答案
相关题目
9.若$\frac{1}{27}$≤x≤9,则f(x)=log3$\frac{x}{27}$•log3(3x)( )
| A. | 有最小值-$\frac{32}{9}$,最大值-3 | B. | 有最小-4,最大值12 | ||
| C. | 有最小值-$\frac{32}{9}$,无最大值 | D. | 无最小值,有最大值12 |
7.函数f(x)=x•2|x|-x-2的零点个数为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
14.将6名留学归国人员分配到济南、青岛两地工作.若济南至少安排2 人,青岛至少安排3人,则不同的安排方法数为( )
| A. | 120 | B. | 150 | C. | 35 | D. | 55 |
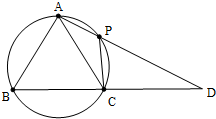 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.