Question

【题目】如图所示，已知椭圆： 的长轴为，过点的直线与轴垂直，椭圆上一点与椭圆的长轴的两个端点构成的三角形的最大面积为2，且椭圆的离心率为.

（1）求椭圆的标准方程；

（2） 设是椭圆上异于， 的任意一点，连接并延长交直线于点， 点为的中点，试判断直线与椭圆的位置关系，并证明你的结论.

Answer 1

【答案】（1）（2）直线与椭圆相切于点，证明见解析

【解析】试题分析： 根据条件和离心率公式可以求得， ，即可求出椭圆的标准方程； 设，由的坐标求得直线的方程，得到点的坐标，又因为

为中点，求出的坐标，得到直线的方程，联立椭圆方程，利用判别式求得结论

解析：（1）依题设条件可得： ， .又，解得， ，所以椭圆的标准方程为.

（2）直线与椭圆相切于点.证明如下：

设点，又，所以直线的方程为.令，得，即点.又点， 为中点，所以.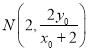

于是直线的方程为 ，即 .

因为，所以，所以 ，整理得到，由消去并整理得到： ，即，此方程的判别式，所以直线与椭圆相切于点.