题目内容
【题目】已知数列{an}中,a1=2,n(an+1﹣an)=an+1,n∈N*.
(1)设bn =![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)若对于任意的t∈[0,1],n∈N*,不等式![]() 2t2﹣(a+1)t+a2﹣a+3恒成立,求实数a的取值范围.
2t2﹣(a+1)t+a2﹣a+3恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题得![]() ,再利用累加法求数列{bn}的通项公式.(2)由题得3≤﹣2t2﹣(a+1)t+a2﹣a+3,即得2t2+(a+1)t﹣a2+a≤0,在t∈[0,1]上恒成立,接着
,再利用累加法求数列{bn}的通项公式.(2)由题得3≤﹣2t2﹣(a+1)t+a2﹣a+3,即得2t2+(a+1)t﹣a2+a≤0,在t∈[0,1]上恒成立,接着
设f(t)=2t2+(a+1)t﹣a2+a,t∈[0,1],得不等式组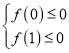 ,解之得解.
,解之得解.
(1)根据题意,数列{an}中,n(an+1﹣an)=an+1,
∴nan+1﹣(n+1)an=1,
∴![]() ,
,
∴![]() ,(n≥2)
,(n≥2)
∴![]() (
(![]() )+(
)+(![]() )+…+(a2﹣a1)+a1,
)+…+(a2﹣a1)+a1,
=(![]() )+(
)+(![]() )+…+(1
)+…+(1![]() )+2=3
)+2=3![]()
∴bn =3![]() .
.
(2)∵![]() 2t2﹣(a+1)t+a2﹣a+3恒成立,且3
2t2﹣(a+1)t+a2﹣a+3恒成立,且3![]() 3,
3,
∴3≤﹣2t2﹣(a+1)t+a2﹣a+3
∴2t2+(a+1)t﹣a2+a≤0,在t∈[0,1]上恒成立,
设f(t)=2t2+(a+1)t﹣a2+a,t∈[0,1],
∴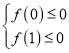 ,即
,即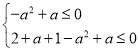 ,
,
解得a≤﹣1或a≥3.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视.从学生体检评价报告单中了解到我校3000名学生的体重发育评价情况如下表:
偏瘦 | 正常 | 偏胖 | |
女生/人 | 300 | 865 | y |
男生/人 | x | 855 | z |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(1)求x的值.
(2)若用分层抽样的方法,从这批学生中随机抽取60名,应在偏胖学生中抽多少名?
(3)已知![]() ,
,![]() ,求偏胖学生中男生不少于女生的概率.
,求偏胖学生中男生不少于女生的概率.