题目内容
【题目】如图,在平面四边形ABCD中,CD=1,BC=2,∠C=120°
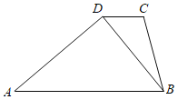
(1)求cos∠CBD的值;
(2)若AD=4,cos∠ABC![]() ,求∠A的大小.
,求∠A的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由余弦定理求出BD![]() ,再利用余弦定理求cos∠CBD的值.(2)先求出sin∠ABD的值,再利用正弦定理求解.
,再利用余弦定理求cos∠CBD的值.(2)先求出sin∠ABD的值,再利用正弦定理求解.
(1)∵在△BCD中,CD=1,BC=2,∠C=120°.
∴由余弦定理可得:BD2=BC2+CD2﹣2BDCDcosC=4+1﹣2×2×1×(![]() )
)![]() ,
,
∴BD![]() ,∴cos∠CBD
,∴cos∠CBD![]() .
.
(2)由(1)可得sin∠CBD![]() ,
,
∵cos∠ABC![]() ,∴sin∠ABC
,∴sin∠ABC![]() ,
,
∴sin∠ABD=sin(∠ABC﹣∠CBD)=sin∠ABCcos∠CBD﹣cos∠ABCsin∠CBD
![]() ,
,
由正弦定理可得![]() ,即sinA
,即sinA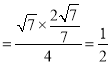 ,
,
∴A![]() 或A
或A![]() ,
,
∵BD<AD,∴A![]() .
.

练习册系列答案
相关题目