题目内容
3.已知函数f(x)=$\frac{x}{{e}^{x}}$,给出下列结论:①(1,+∞)是f(x)的单调递减区间;
②当k∈(-∞,$\frac{1}{e}$)时,直线y=k与y=f(x)的图象有两个不同交点;
③函数y=f(x)的图象与y=x2+1的图象没有公共点.
其中正确结论的序号是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
分析 ①先求出函数的导数,令导函数小于0,解出即可判断;②根据函数的单调性画出函数的图象,通过图象读出即可;③求出f(x)的最大值小于y=x2+1的最小值,从而得到答案.
解答 解:①f′(x)=$\frac{1-x}{{e}^{x}}$,令f′(x)<0,解得:x>1,
∴函数f(x)在(1,+∞)递减,
故①正确;
②∵f(x)在(-∞,1)递增,在(1,+∞)递减,
∴f(x)max=f(1)=$\frac{1}{e}$,
x→-∞时,f(x)→-∞,x→+∞时,f(x)→0,
画出函数f(x)的图象,如图示: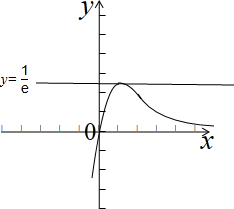 ,
,
∴当k∈(-∞,0)时,直线y=k与y=f(x)的图象有1个不同交点,
当k∈(0,$\frac{1}{e}$)时,直线y=k与y=f(x)的图象有两个不同交点,
故②错误;
③函数f(x)≤$\frac{1}{e}$,而y=x2+1≥1,
∴函数y=f(x)的图象与y=x2+1的图象没有公共点,
故③正确;
故选:①③.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
14.若f(x)=|lgx|,当a<b<c时,f(a)>f(c)>f(b).则下列不等式中正确的为( )
| A. | (a-1)(c-1)>0 | B. | ac>1 | C. | ac=1 | D. | ac<1 |
18.要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有( )
| A. | 48种 | B. | 36种 | C. | 18种 | D. | 12种 |
15.某小组有10名学生,其中女生3名,从中选3名代表,要求至少有1名女生,则不同的选法种数是( )
| A. | 85 | B. | 100 | C. | 108 | D. | 120 |
 的图象关于直线
的图象关于直线 对称,则
对称,则 的最大值为 .
的最大值为 .