题目内容
19.在△ABC中,角A,B,C所对的边分别为a,b,c,设△ABC的面积为S,下列条件不能推出B≤60°的是( )| A. | a,b,c成等比数列 | B. | a,b,c成等差数列 | C. | 1+2cos2B≥0 | D. | S≤$\frac{\sqrt{3}}{4}$(a2+c2-b2) |
分析 由题意,判断选项是否推出cosB$≥\frac{1}{2}$即可.
解答 解:对于A,a,b,c成等比数列,则b2=ac,所以cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-ac}{2ac}≥\frac{2ac-ac}{2ac}=\frac{1}{2}$,所以B≤60°;
对于B,a,b,c成等差数列,则2b=a+c,所以cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{3{(a}^{2}+{c}^{2})-2ac}{8ac}≥\frac{6ac-2ac}{8ac}=\frac{1}{2}$,所以B≤60°;
对于C,1+2cos2B≥0,则cos2B≥$-\frac{1}{2}$,所以0≤2B≤120°或者240°≤2B<360°,所以B≤60°或者120°≤B<180°;
对于D,由S≤$\frac{\sqrt{3}}{4}$(a2+c2-b2)得到$\frac{1}{2}$acsinB≤$\frac{\sqrt{3}}{4}$(2accosB),所以0<tanB≤$\sqrt{3}$,得到B≤60°.
故选C.
点评 本题考查了利用余弦定理解三角形、利用基本不等式求最值.

练习册系列答案
相关题目
10.设数列{an}的通项公式为:an=n2+kn(n∈N+),若数列{an}是单调递增数列,则实数k的取值范围是( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | [-3,+∞) | D. | (-3,+∞) |
14.若f(x)=|lgx|,当a<b<c时,f(a)>f(c)>f(b).则下列不等式中正确的为( )
| A. | (a-1)(c-1)>0 | B. | ac>1 | C. | ac=1 | D. | ac<1 |
 .
.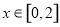 时,函数
时,函数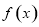 恒有意义,求实数
恒有意义,求实数 的取值范围;
的取值范围; ,使得函数
,使得函数 在区间
在区间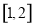 上为减函数,并且最大值为1?如果存在?试求出
上为减函数,并且最大值为1?如果存在?试求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.