题目内容
4.已 知椭圆C1::$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与双曲线C2有公共焦点F1、F2,(F1、F2分别为左、右焦点),它们在第一象限交于点M,离心率分别为e1和e2,线段MF1的垂直平分线过F2,则$\frac{1}{e_1}+\frac{e_2}{2}$的最小值为$2+\sqrt{2}$.分析 通过图象可知F1F2=F2M=2c,利用椭圆、双曲线的定义及离心率公式可得$\frac{1}{e_1}+\frac{e_2}{2}$=2+$\frac{{a}_{2}}{c}$+$\frac{c}{2{a}_{2}}$,通过基本不等式即得结论.
解答 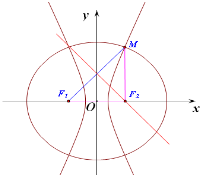 解:由题意可知:F1F2=F2M=2c,
解:由题意可知:F1F2=F2M=2c,
又∵F1M+F2M=2a1,F1M-F2M=2a2,
∴F1M+2c=2a1,F1M-2c=2a2,
两式相减,可得:a1-a2=2c,
∵$\frac{1}{e_1}+\frac{e_2}{2}$=$\frac{{a}_{1}}{c}$+$\frac{c}{2{a}_{2}}$=$\frac{2{a}_{1}{a}_{2}+{c}^{2}}{2c{a}_{2}}$,
∴$\frac{1}{e_1}+\frac{e_2}{2}$=$\frac{2(2c+{a}_{2}){a}_{2}+{c}^{2}}{2c{a}_{2}}$=$\frac{4c{a}_{2}+2{{a}_{2}}^{2}+{c}^{2}}{2c{a}_{2}}$=2+$\frac{{a}_{2}}{c}$+$\frac{c}{2{a}_{2}}$,
∵$\frac{{a}_{2}}{c}$+$\frac{c}{2{a}_{2}}$≥2$\sqrt{\frac{{a}_{2}}{c}•\frac{c}{2{a}_{2}}}$=2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$,当且仅当$\frac{{a}_{2}}{c}$=$\frac{c}{2{a}_{2}}$时等号成立,
∴$\frac{1}{e_1}+\frac{e_2}{2}$的最小值为2+$\sqrt{2}$,
故答案为:$2+\sqrt{2}$.
点评 本题考查椭圆的简单性质,考查运算求解能力,注意解题方法的积累,属于中档题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | (0,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-1,+∞) | D. | (-∞,-1)∪(0,+∞) |
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
| A. | -4 | B. | 4 | C. | 14 | D. | -14 |
| A. | ?x0∈R,x02+2x0+2>0 | B. | ?x∈R,x2+2x+2≤0 | ||
| C. | ?x∈R,x2+2x+2>0 | D. | ?x∈R,x2+2x+2≥0 |