题目内容
19.已知等比数列{an}满足an+1+an=4×3n-1(n∈N*).(I)求数列{an}的通项公式;
(Ⅱ)若bn=log3an,求Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.
分析 (I)设等比数列{an}的公比为q,由an+1+an=4×3n-1(n∈N*).可得$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}=4}\\{{a}_{1}{q}^{2}+{a}_{1}q=12}\end{array}\right.$,解得即可得出;
(II)bn=log3an=n-1.可得b2n-1b2n-b2nb2n+1=b2n(b2n-1-b2n+1)=2-4n.再利用等差数列的前n项和公式即可得出.
解答 解:(I)设等比数列{an}的公比为q,由an+1+an=4×3n-1(n∈N*).
可得$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}=4}\\{{a}_{1}{q}^{2}+{a}_{1}q=12}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{q=3}\end{array}\right.$,
∴a3=3n-1.
(II)bn=log3an=n-1.
b2n-1b2n-b2nb2n+1=b2n(b2n-1-b2n+1)=(2n-1)(-2)=2-4n.
∴Tn=(2-4×1)+(2-4×2)+…+(2-4n)=$\frac{(-2+2-4n)n}{2}$=-2n2.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.一种集合A={3,5,x},B={2},若A∪B=A,则实数x的值为( )
| A. | -2 | B. | 2 | C. | 3 | D. | 5 |
11.已知随机变量ξ服从正态分布N(2,1),若P(ξ>3)=0.023,则P(1≤ξ≤3)=( )
| A. | 0.046 | B. | 0.623 | C. | 0.977 | D. | 0.954 |

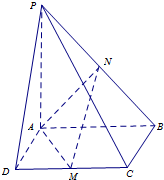 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.