给定函数①$y={x^{\frac{1}{2}}}$.②$y={log {\frac{1}{2}}}$.③y=|x+1|.④y=-2x+1.其中在区间(0.1)上单调递减的函数序号是( )A．①②B．②③C．②④D．③④ 题目和参考答案——青夏教育精英家教网—

题目内容

12．给定函数①$y={x^{\frac{1}{2}}}$，②$y={log_{\frac{1}{2}}}（{x+1}）$，③y=|x+1|，④y=-2^x+1，其中在区间（0，1）上单调递减的函数序号是（　　）

A．

①②

B．

②③

C．

②④

D．

③④

分析根据基本初等函数的单调性，对题目中函数的单调性进行判断即可．

解答解：对于①，函数$y={x^{\frac{1}{2}}}$在[0，+∞）上是单调增函数，∴不满足题意；
对于②，函数$y={log_{\frac{1}{2}}}（{x+1}）$，在（-1，+∞）上是单调减函数，∴满足题意；
对于③，函数y=|x+1|在[-1，+∞）上是单调增函数，∴不满足题意；
对于④，函数y=-2^x+1在（-∞，+∞）上是单调减函数，∴满足题意；
综上，满足在区间（0，1）上单调递减的函数序号是②④．
故选：C．

点评本题考查了基本初等函数单调性的应用问题，解题时应熟记常见的基本初等函数的图象与性质，是基础题目．

练习册系列答案

3．阅读如图所示的程序框图．若输入n=5，则输出k的值为2．

20．一个多边形的周长等于158cm，所有各边的长成等差数列，最大边的长等于44cm，公差等于3cm，求多边形的边数．

7．如图展示了一个由区间（0，1）到实数集R的映射过程；区间（0，1）中的实数x对应数轴上的点M，如图①；将线段AB围成一个圆，使两端点A，B恰好重合，如图②；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），如图③．图③中直线AM与x轴交于点N（n，0），则x的象就是n，记作f（x）=n．

下列说法中正确的序号是①③⑤．（填上所有正确命题的序号）
①f（x）在定义域上单调递增；
②f（x）的图象关于y轴对称；
③$\frac{1}{2}$是f（x）的零点；
④$f（{\frac{1}{3}}）+f（{\frac{2}{3}}）=1$；
⑤f（x）＞1的解集是$（{\frac{3}{4}，1}）$．

17．某地举行了一场小型公车拍卖会，轿车拍卖成交了4辆，成交价格分别为3万元，x万元，7万元，9万元；货车拍卖成交了2辆，成交价格分别为7万元，8万元．总平均成交价格为7万元．
（I）求该场拍卖会成交价格的中位数；
（Ⅱ）某人拍得两辆车，求拍得轿车、货车各一辆且总成交价格不超过14万元的概率．

4．已知椭圆C₁：：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）与双曲线C₂有公共焦点F₁、F₂，（F₁、F₂分别为左、右焦点），它们在第一象限交于点M，离心率分别为e₁和e₂，线段MF₁的垂直平分线过F₂，则$\frac{1}{e_1}+\frac{e_2}{2}$的最小值为$2+\sqrt{2}$．

1．已知函数f（x）=cos（2x-$\frac{π}{3}$），g（x）=sin2x，将函数f（x）的图象经过下列哪种可以与g（x）的图象重合（　　）

	A．	向左平移$\frac{π}{12}$个单位		B．	向左平移$\frac{π}{6}$个单位
	C．	向右平移$\frac{π}{12}$个单位		D．	向右平移$\frac{π}{6}$个单位

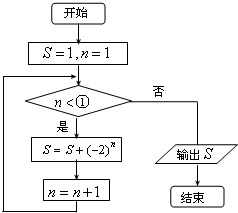
2．阅读下面程序框图，为使输出的数据为11，则①处应填的数字可以为（　　）

试题分类