题目内容
【题目】已知数列![]() 满足
满足![]() ,函数
,函数![]() 是定义在
是定义在![]() 上的奇函数,且满足
上的奇函数,且满足![]() .
.
(Ⅰ)确定![]() 与
与![]() 的关系式,并求
的关系式,并求![]() 的解析式.
的解析式.
(Ⅱ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,是否存在实数
,是否存在实数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)存在,
(Ⅱ)存在,![]() 的最大值为0.
的最大值为0.
【解析】
(Ⅰ)根据函数![]() 是定义在
是定义在![]() 上的奇函数,且数列
上的奇函数,且数列![]() 满足
满足![]() 及
及![]() ,可得
,可得![]() ,从而可得
,从而可得![]() 为等比数列,并得出
为等比数列,并得出![]() 的解析式;
的解析式;
(Ⅱ)由![]() 求出
求出![]() ,递推公式代入可得
,递推公式代入可得![]() ,由裂项求和可得
,由裂项求和可得![]() ,代入不等式分离参数,转化为函数最值问题即可求解
,代入不等式分离参数,转化为函数最值问题即可求解![]() 的最大值.
的最大值.
(Ⅰ)∵函数![]() 是定义在
是定义在![]() 上的奇函数,且数列
上的奇函数,且数列![]() 满足
满足![]() ,
,
∴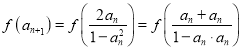 ,而
,而![]() .
.
∴![]() .
.
又![]() ,∴
,∴![]() ,∴
,∴ ,
,![]() 为等比数列.
为等比数列.
∴![]() .
.
(Ⅱ)∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴
![]() .
.
∴![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即![]() 对于任意的
对于任意的![]() 恒成立,
恒成立,
∵![]() 关于
关于![]() 单调递减且
单调递减且![]() 恒成立,
恒成立,
∴![]() .
.
∴![]() 的最大值为0.
的最大值为0.

 阅读快车系列答案
阅读快车系列答案【题目】又到了品尝小龙虾的季节,小龙虾近几年来被称作是“国民宵夜”风靡国内外.在巨大的需求市场下,湖北的小龙虾产量占据了全国的半壁江山,湖北某地区近几年的小龙虾产量统计如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: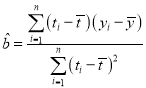 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位).
,计算结果保留小数点后两位).
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
