��Ŀ����
����Ŀ������ԲE��![]() 1��a��b��0����һ����P��ԲO��x2+y2��b2����������PA��PB���е�ֱ���A��B��ֱ��AB�ֱ���x�ᣬy�ύ�ڵ�M��N��OΪ����ԭ�㣩��
1��a��b��0����һ����P��ԲO��x2+y2��b2����������PA��PB���е�ֱ���A��B��ֱ��AB�ֱ���x�ᣬy�ύ�ڵ�M��N��OΪ����ԭ�㣩��

��1��������ԲE�ϴ��ڵ�P������PA��PB������ԲE�������ʵ�ȡֵ��Χ��
��2����֤������ԲE�ڣ�����һ��C����|CO|��|CA|��|CP|��|CB|��
��3������ԲE�Ķ��᳤Ϊ2����MON�������СֵΪ![]() ������ԲE�ķ��̣�
������ԲE�ķ��̣�
���𰸡���1��[![]() ��1������2����������3��
��1������2����������3��![]() ��
��
��������
��1���������֪![]() ������
������![]() ����
����![]() ����Ϊ
����Ϊ![]() ���г�����ʽ��⼴�ɵõ�����𰸣�
���г�����ʽ��⼴�ɵõ�����𰸣�
��2������CΪOP���е�ʱ����ֱ�������ε����ʣ�б���ϵ����ߵ���б�ߵ�һ�룬���ɵõ���C�������⣻
��3���������֪![]() �������P���꣬�����
�������P���꣬�����![]() Ϊֱ����Բ�ķ��̣���ԲO�ķ�������ù��е�
Ϊֱ����Բ�ķ��̣���ԲO�ķ�������ù��е�![]() ��ֱ�߷��̣��������
��ֱ�߷��̣��������![]() �����꣬�������
�����꣬�������![]() ���������O��ֱ��MN�ľ���d������
���������O��ֱ��MN�ľ���d������![]() ���ٽ�ϵ�P����Բ
���ٽ�ϵ�P����Բ![]() ���Լ���������ʽ���õ�
���Լ���������ʽ���õ�![]() ���Ӷ����
���Ӷ����![]() �����ɵõ������.
�����ɵõ������.
��1����![]() ����
����![]() ��
��
�֡�![]() ����
����![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
�֡�![]() ����
����![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
����ԲE�������ʵ�ȡֵ��ΧΪ��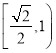 ��
��
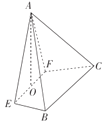
��2��֤��������CΪOP���е�ʱ��
��ֱ��PA��ֱ��PB����ԲO���У�
��![]() ����ֱ�������Σ�
����ֱ�������Σ�
��![]() ����
����![]() ��
��
������ԲE�ڣ�����һ��C����![]() ��
��
��3���������֪![]() �����
�����![]() ��
��
����![]() Ϊֱ����Բ�ķ���Ϊ
Ϊֱ����Բ�ķ���Ϊ![]() ����ԲO�ķ���
����ԲO�ķ���![]() ����ã�
����ã�![]() ��
��
����е�![]() ��ֱ�߷���Ϊ��
��ֱ�߷���Ϊ��![]() ��
��
��![]() �ã�
�ã�![]() ����
����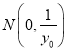 ����
����![]() �ã�
�ã�![]() ����
����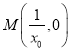 ��
��
��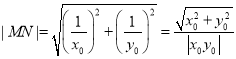 ��
��
�ߵ�O��ֱ��MN�ľ���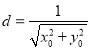 ��
��
��![]() ��
��
�ߵ�P����Բ![]() �ϣ�
�ϣ�
��![]() �����ҽ���
�����ҽ���![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
��![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
����ԲE�ķ���Ϊ��![]() ��
��

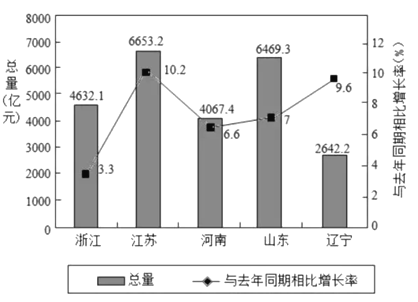
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�����Ŀ�����ض�ͬʱ��A��B��C������ͬ�������ڵ�ij����Ʒ���г�����⣬�Ӹ��������ڴ�����Ʒ������(��λ����)�����ʾ��������Ա�÷ֲ�����ķ�������Щ��Ʒ�й���ȡ6����Ʒ���м�⣮
���� | A | B | C |
���� | 50 | 150 | 100 |
��1������6����Ʒ������A��B��C��������Ʒ��������
��2��������6����Ʒ�������ȡ2�������������н�һ����⣬����2����Ʒ������ͬ�����ĸ��ʣ�
����Ŀ��2019��������������Ϯ����Ȼ���˶��˽������������˳�����ʳ����������µIJ�����������Ȼ���赲����Ʒ�����ı���.���ڣ�ij֪������Ʒ���۹�˾ͨ����������ķ�ʽ���õ���100�Ҽ��˳���3���ڽ����ܼ۵�ͳ�ƽ�����±���ʾ��
���(��λ����Ԫ�� |
|
|
|
|
|
|
Ƶ�� | 3 | 11 | 20 | 27 | 26 | 13 |
(1)��Ƶ���ֲ������¿�����Ϊ������鳬��3���ڽ����ܼ�![]() ��������Ϊ��100�ҳ���3���ڽ����ܼ۵�ƽ��ֵ(ͬһ���е������ø���������е�ֵ����������������̬�ֲ�����
��������Ϊ��100�ҳ���3���ڽ����ܼ۵�ƽ��ֵ(ͬһ���е������ø���������е�ֵ����������������̬�ֲ�����![]() ��
��
(2)��(1)�������£��ù�˾Ϊ�������۶�ر�Ϊ��100�ҳ����ƶ����³齱������
����m��ʾ������3���ڽ����ܼ۳������İٷֵ���������![]() .��
.��![]() ����ó��л��1�γ齱���
����ó��л��1�γ齱���![]() ����ó��л��2�γ齱���
����ó��л��2�γ齱���![]() ����ó��л��3�γ齱���
����ó��л��3�γ齱���![]() ����ó��л��4�γ齱���
����ó��л��4�γ齱���![]() ����ó��л��5�γ齱���
����ó��л��5�γ齱���![]() ����ó��л��6�γ齱����.���⣬�涨3���ڽ����ܼ۵������ij���û�г齱���
����ó��л��6�γ齱����.���⣬�涨3���ڽ����ܼ۵������ij���û�г齱���
��ÿ�γ齱�н���õĽ�����Ϊ1000Ԫ��ÿ�γ齱�н��ĸ���Ϊ![]() .
.
�賬��A�μ��˳�飬�ҳ���A��3���ڽ����ܼ�![]() ��Ԫ.��X����λ��Ԫ)��ʾ����A��õĽ����ܶ��X�ķֲ�������ѧ����.
��Ԫ.��X����λ��Ԫ)��ʾ����A��õĽ����ܶ��X�ķֲ�������ѧ����.
���ο������빫ʽ��![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() .
.