题目内容
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() .
.
(1) 若![]() 是函数
是函数![]() 的导函数,当
的导函数,当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2) 若![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围;
的取值范围;
(3) 当![]() 时,求整数
时,求整数![]() 的所有值,使方程
的所有值,使方程![]() 在
在![]() 上有解.
上有解.
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求导数,所求不等式可化为ax2+(2a+1)x>0然后可求;
(2)![]() 在
在![]() 上是单调增函数转化为
上是单调增函数转化为![]() 在
在![]() 恒成立,结合根的分布求解;
恒成立,结合根的分布求解;
(3)根据零点存在定理和单调性,先确定零点所在区间,然后确定![]() 的值.
的值.
(1) f′(x)=[ax2+(2a+1)x+1]·ex.
不等式f′(x)>ex可化为[ax2+(2a+1)x]·ex>0.
因为ex>0,故有ax2+(2a+1)x>0.
当a>0时,不等式f′(x)>ex的解集是![]() .
.
(2) 由(1)得f′(x)=[ax2+(2a+1)x+1]·ex.
① 当a=0时,f′(x)=(x+1)ex,f′(x)>0在[-1,1]上恒成立,
当且仅当x=-1时取等号,故a=0符合要求;
② 当a≠0时,令g(x)=ax2+(2a+1)x+1,
因为Δ=(2a+1)2-4a=4a2+1>0,
所以g(x)=0有两个不相等的实数根x1,x2,不妨设x1>x2,
因此f(x)既有极大值又有极小值.
若a>0,因为g(-1)·g(0)=-a<0,所以f(x)在(-1,1)上有极值点.
故f(x)在[-1,1]上不单调.
若a<0,可知x1>0>x2,
因为g(x)的图象开口向下,要使f(x)在[-1,1]上单调,又g(0)=1>0,
必须满足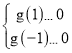 ,即
,即![]() ,解得
,解得![]() ≤a<0.
≤a<0.
综上所述,a的取值范围是![]() .
.
(3) 当a=0时,方程即为xex=x+2,由于ex>0,所以x=0不是方程的解,
所以原方程等价于ex-![]() -1=0,令h(x)=ex-
-1=0,令h(x)=ex-![]() -1.
-1.
因为h′(x)=ex+![]() >0对于x∈(-∞,0)∪(0,+∞)恒成立,
>0对于x∈(-∞,0)∪(0,+∞)恒成立,
所以h(x)在(-∞,0)和(0,+∞)上是单调增函数.
又h(1)=e-3<0,h(2)=e2-2>0,h(-3)=e-3-![]() <0,h(-2)=e-2>0,
<0,h(-2)=e-2>0,
所以方程f(x)=x+2有且只有两个实数根,
且分别在区间[1,2]和[-3,-2]上,
所以整数k的所有值为{-3,1}.